Ισορροπία και κίνηση στερεού. Ένα φύλλο εργασίας.

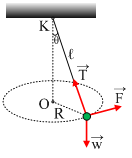
Μια ομογενής δοκός ΑΒ, μήκους ℓ, ισορροπεί, όπως στο σχήμα, αρθρωμένη στο άκρο της Α, ενώ το άλλο της άκρο Β, είναι δεμένο με νήμα που σχηματίζει γωνία θ=30° με τη δοκό.

i)  Να σχεδιάστε τις δυνάμεις που ασκούνται πάνω της.

ii) Ποιες από τις παρακάτω προτάσεις είναι σωστές και ποιες λάθος.

α) Η ροπή του βάρους ως προς το άκρο Α είναι ίση με –w∙ℓ/2.

β) Η ροπή της τάσης του νήματος ως προς το άκρο Α είναι ίση με w∙ℓ/2.

γ) Η ροπή της δύναμης F που δέχεται η δοκός από την άρθρωση, ως προς το άκρο Β έχει τιμή –w∙ℓ/2.

δ) Η ροπή της δύναμης F που δέχεται η δοκός από την άρθρωση, ως προς το σημείο Γ  έχει τιμή  w∙ℓ/2.

ε)  Η δύναμη F σχηματίζει γωνία 30° με τη δοκό.

Δείτε όλο το φύλλο εργασίας σε pdf  αλλά και σε Word.

Και σύντομες απαντήσεις

Μπορούμε να φωτίσουμε το σημείο;

Διαθέτουμε ένα δοχείο με βάθος h=40cm, το οποίο είναι γεμάτο πλήρως με υγρό με δείκτη διάθλασης η=√2, για μια μονοχρωματική ακτινοβολία φωτός, που παράγεται από μια συσκευή Laser. Στο πάνω μέρος, είναι καλυμένη με αδιαφανές κάλυμα, η μισή ελεύθερη επιφάνεια του δοχείου, όπως στο σχήμα. Στον πυθμένα του δοχείου υπάρχουν δύο σημεία Α και Β, όπως στο σχήμα, όπου (ΑΒ)=40cm.

i) Μια ακτίνα φωτός φτάνει στο σημείο Α, αφού διαθλαστεί στο σημείο Κ, όπου (ΜΚ)=30cm.  Να βρεθεί η γωνία πρόσπτωσης φ.

 ii) Μπορούμε να ρίξουμε φως στην ελεύθερη επιφάνεια του υγρού, σε σημείο Λ δεξιά του Κ και να φωτίσουμε το σημείο Α ;

iii) Να εξετάσετε αν θα μπορούσαμε να φωτίσουμε το σημείο Β, με χρήση ακτίνας από την ίδια συσκευή Laser.

Απάντηση:

Μπορούμε να φωτίσουμε το σημείο

Άλλο ένα στάσιμο σε χορδή και η εξίσωσή του.

Μια χορδή με σταθερά άκρα διεγείρεται οπότε δημιουργείται πάνω της ένα στάσιμο κύμα με 7 δεσμούς (εκτός των δύο άκρων). Η πρώτη κοιλία Κ₁ απέχει 3cm από το αριστερό άκρο της χορδής και τη στιγμή που θεωρούμε t=0, έχει μέγιστη ταχύτητα με τιμή 40π cm/s, ενώ τη στιγμή t₁=0,05s η ταχύτητά της είναι υ₁=-40π cm/s, για πρώτη φορά.

i)   Να βρεθεί το πλάτος ταλάντωσης της κοιλίας Κ₁, καθώς και το μήκος L της χορδής.

ii)  Να βρεθεί η εξίσωση του στάσιμου κύματος, θεωρώντας ότι η πρώτη κοιλία βρίσκεται στη θέση x=0.

iii)Να σχεδιάστε στιγμιότυπα της χορδής τις χρονικές στιγμές t₂=1/40s και t₃=1/16s, στο ίδιο σύστημα αξόνων.

iv) Να βρεθεί η εξίσωση του ίδιου στάσιμου, θεωρώντας x=0 το αριστερό άκρο της χορδής.

Άλλο ένα στάσιμο σε χορδή και η εξίσωσή του

Άλλο ένα στάσιμο σε χορδή και η εξίσωσή του

Ροπές σε ένα κωνικό εκκρεμές.

Ένα μικρό σώμα είναι δεμένο στο άκρο νήματος μήκους ℓ και κρέμεται από ένα σημείο Κ. Το σώμα με την επίδραση μιας οριζόντιας δύναμης F, διαγράφει οριζόντιο κύκλο κέντρου Ο. Σε μια στιγμή η ακτίνα του κύκλου είναι R= ½ ℓ, ενώ η δύναμη F  είναι κάθετη στο νήμα και εφαπτόμενη του οριζόντιου κύκλου.

i)  Η ροπή του βάρους ως προς το κέντρο Ο του κύκλου, είναι οριζόντια

ii)  Η ροπή του βάρους ως προν τον άξονα ΟΚ έχει την κατεύθυνση του άξονα.

iii) Η ροπή της δύναμης F είναι ίδια, είτε μετριέται ως προς τα σημεία Ο και Κ, είτε ως προς τον άξονα ΟΚ.

iv)  Η ροπή της τάσης του νήματος ως προς τον άξονα ΟΚ είναι μηδενική, ενώ ως προς το σημείο Ο έχει μέτρο ½ mgl.

Απάντηση

Ροπές σε ένα κωνικό εκκρεμές.

Ροπή δύναμης. Φύλλο εργασίας.

Ένα μικρό σώμα είναι δεμένο στο άκρο νήματος μήκους ℓ και κρέμεται από ένα σημείο Κ. Το σώμα με την επίδραση μιας οριζόντιας δύναμης F, διαγράφει οριζόντιο κύκλο κέντρου Ο και ακτίνας R. Η δύναμη F  είναι διαρκώς κάθετη στο νήμα και εφαπτόμενη του οριζόντιου κύκλου. Να υπολογιστούν τα μέτρα των ροπών:

i)  Της δύναμης F, ως προς:        

α) το κέντρο Ο                 β) το σημείο Κ           γ) τον άξονα (ΚΟ)

ii) Της τάσης του νήματος ως προς:        

α) το κέντρο Ο                 β) το σημείο Κ          γ) τον άξονα (ΚΟ)

iii) Του βάρους, ως προς:

α) το κέντρο Ο                 β) το σημείο Κ          γ) τον άξονα (ΚΟ)

iv)  Ποιες προτάσεις είναι σωστές και ποιες λάθος:

a)   Η ροπή της F ως προς το σημείο Ο είναι κατακόρυφη.

b)   Η ροπή της F ως προς το σημείο Κ είναι κατακόρυφη.

c)   Η ροπή της F ως προς τον άξονα ΟΚ είναι κατακόρυφη.

d)   Η ροπή του βάρους ως προς το Ο είναι οριζόντια.

e)   Η ροπή του βάρους ως προς τον άξονα ΟΚ είναι μηδενική.

f)    Η ροπή της τάσης ως προς το Ο είναι οριζόντια και αντίθετη της ροπής του βάρους.

g)   Η ροπή της τάσης ως προς τον άξονα ΟΚ είναι οριζόντια.

Δείτε όλο το φύλλο εργασίας σε pdf  ή κατεβάστε για επεξεργασία σε Word.

Κινηματική Στερεού Σώματος. Ένα φύλλο εργασίας.

Στο παρακάτω σχήμα δίνεται ένας τροχός που κινείται. Σε ποια ή ποιες περιπτώσεις ο τροχός:

i)       εκτελεί μόνο στροφική κίνηση;	ii)     κυλίεται χωρίς να ολισθαίνει;
iii)    μεταφέρεται χωρίς να στρέφεται.	iv)   εκτελεί σύνθετη κίνηση.
v)    στρέφεται αλλά και ολισθαίνει	vi)   σπινάρει.

Δείτε όλο το φύλλο εργασίας σε pdf  ή μπορείτε να το κατεβάσετε για επεξεργασία σε Word.

Κυκλική-Στροφική κίνηση. Ένα φύλλο εργασίας.

Ένα σώμα είναι δεμένο στο άκρο νήματος, το άλλο άκρο του οποίου είναι δεμένο στο σημείο Ο. Αφήνουμε το σώμα να κινηθεί από την θέση (1), όπου το τεντωμένο νήμα είναι οριζόντιο.

Για την θέση (2) που το νήμα σχηματίζει γωνία θ με την οριζόντια διεύθυνση:

i)   Να σχεδιάστε στο διπλανό σχήμα τα διανύσματα της ταχύτητας, της κεντρομόλου και επιτρόχιας επιτάχυνσης, της γωνιακής ταχύτητας  και της γωνιακής επιτάχυνσης.

ii)  Να σχεδιάστε επίσης τα ίδια διανύσματα όπως παραπάνω για τις θέσεις (3) και (4), όπου στην θέση (3) το νήμα είναι κατακόρυφο, ενώ στην θέση (4) το σώμα έχει προχωρήσει σχηματίζοντας το νήμα γωνία φ με την κατακόρυφη.

Δείτε όλο το φύλλο εργασίας σε pdf αλλά και σε Word. 

Δυο κύματα διαδίδονται αντίθετα

Κατά μήκος ενός γραμμικού ελαστικού μέσου διαδίδονται δύο κύματα με αντίθετες διευθύνσεις και σε μια στιγμή την οποία θεωρούμε ότι t₀=0, η εικόνα του μέσου, είναι αυτή του παρακάτω σχήματος.

Το πλάτος των κυμάτων είναι Α=0,5m, το μήκος κύματος λ=2m, ενώ το κύμα που διαδίδεται προς τα αριστερά φτάνει στο σημείο Ο τη στιγμή t₁=0,5s. Θεωρώντας ότι το σημείο Ο βρίσκεται στη θέση x=0 και (ΟΒ)=1m:

i)  Να βρεθούν οι εξισώσεις των δύο κυμάτων.

ii) Να βρεθεί η εξίσωση της απομάκρυνσης των διαφόρων σημείων του μέσου στην περιοχή 0 ≤ x ≤ 4m, μετά από την συμβολή των δύο αυτών κυμάτων.

iii) Να παραστήσετε στο ίδιο σύστημα αξόνων την απομάκρυνση των διαφόρων σημείων της παραπάνω περιοχής τις χρονικές στιγμές t₂=2s και t₃=2,5s.

iv) Να βρεθεί η διαφορά φάσης μεταξύ δύο σημείων Β και Γ στις θέσεις 1,2m και 1,5m για t ≥2s.

Απάντηση:

Δυο κύματα διαδίδονται αντίθετα.

Διαγώνισμα στις ταλαντώσεις. 2011-12

Ένα σώμα πραγματοποιεί ταυτόχρονα δύο ταλαντώσεις της ίδιας  διεύθυνσης, γύρω από την ίδια θέση ισορροπίας με εξισώσεις:

x₁= 0,1ημ100πt   (μονάδες στο S.I.)

x₂= 0,1 ημ(102πt+π)  (μονάδες στο S.I.)

i)  Να βρεθεί η εξίσωση κίνησης του σώματος.

ii) Να βρεθεί η διαφορά φάσης μεταξύ των δύο ταλαντώσεων σε συνάρτηση με το χρόνο και να γίνει η γραφική της παράσταση.

iii) Να βρεθούν οι χρονικές στιγμές t₁ που t₂ που η διαφορά φάσης μεταξύ των δύο ταλαντώσεων παίρνει τις τιμές:

        α) Δφ₁=2π  και   β)  Δφ₂=5π

iv) Για το χρονικό διάστημα t₁≤ t ≤ t₂ να βρεθούν:

α) Ο αριθμός μεγίστων του πλάτους ( πόσες φορές η περιβάλλουσα παίρνει μέγιστη τιμή κατ' απόλυτο τιμή)

β)  Ο αριθμός των ταλαντώσεων που πραγματοποίησε το σώμα.

Δείτε όλο το διαγώνισμα από εδώ.

Διαγώνισμα στις ταλαντώσεις. 2011-12

Κύμα προς τ' αριστερά, φάση και στιγμιότυπα.

Κατά μήκος ενός γραμμικού ελαστικού μέσου και από δεξιά προς τ' αριστερά διαδίδεται ένα κύμα πλάτους  Α=0,1m και μήκους κύματος λ=1m. Τη χρονική στιγμή t₀=0 το κύμα φτάνει στο σημείο Ο, στη θέση x=0, οπότε το σημείο αυτό αρχίζει την ταλάντωσή του, κινούμενο προς την θετική κατεύθυνση και φτάνει στην ακραία θέση της ταλάντωσης τη στιγμή t₁=0,5s. Θεωρούμε την προς τα δεξιά κατεύθυνση θετική.

i) Να βρεθεί η εξίσωση του κύματος.

ii) Να σχεδιάστε  στιγμιότυπα του κύματος  για μια περιοχή μεταξύ των σημείων Β και Γ του μέσου στις θέσεις  x_B =2,5m και x_Γ=-2m, τις χρονικές στιγμές t₁=2s και  t₂ = 5,5s.

iii) Να κάνετε τη γραφική παράσταση της φάσης του σημείου Β σε συνάρτηση με το χρόνο.

Απάντηση:

Κύμα προς τ_ αριστερά, φάση και στιγμιότυπα.

Από το στιγμιότυπο κύματος σε ταλάντωση σημείου.

Στο παραπάνω σχήμα δίνονται δύο στιγμιότυπα ενός αρμονικού κύματος, τα οποία διαφέρουν χρονικά κατά Δt=0,25s και για τα σημεία δεξιά της θέσης x=0.

Αν το σημείο Γ του σχήματος ξεκίνησε την ταλάντωσή του τη χρονική στιγμή t₀=0, να βρεθούν:

i)  Το μήκος και η περίοδος του κύματος.

ii) Η εξίσωση του κύματος.

iii) Η εξίσωση της απομάκρυνσης σε συνάρτηση με το χρόνο, ενός σημείου Β, η φάση του οποίου υπολείπεται κατά 7π/6 της φάσης του σημείου Γ.

iv) Να γίνει η γραφική παράσταση της επιτάχυνσης του σημείου Β σε συνάρτηση με το χρόνο.

Απάντηση:

Από το στιγμιότυπο κύματος σε ταλάντωση σημείου.