Μια ράβδος στο άκρο νήματος

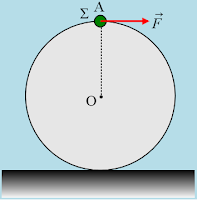
Μια ομογενής ράβδος μήκους ℓ=0,4m και μάζας m=0,6kg έχει προσδεθεί στο μέσον της Μ, μέσω αμελητέου βάρους και μη εκτατού νήματος, μήκους d=1m, με σταθερό σημείο Ο. Η ράβδος συγκρατείται στη θέση που δείχνει το σχήμα, όπου το νήμα είναι τεντωμένο σχηματίζοντας γωνία θ με την κατακόρυφο, όπου ημθ=0,6, ενώ το νήμα είναι κάθετο στη ράβδο. Σε μια στιγμή αφήνουμε τη ράβδο ελεύθερη να κινηθεί. Να βρεθούν:

i)   Οι αρχικές επιταχύνσεις του μέσου Μ και των δύο άκρων Α και Β της ράβδου.

ii)  Ο αρχικός ρυθμός μεταβολής της στροφορμής της ράβδου, ως προς οριζόντιο άξονα:

α) Ο οποίος περνά από το σημείο πρόσδεσης Ο.

β) Ο οποίος είναι κάθετος στη ράβδο, στο μέσον της Μ.

iii)  Να σχεδιάστε τη ράβδο τη στιγμή που το νήμα γίνεται κατακόρυφο και για τη θέση αυτή να υπολογιστούν:

α) Οι ταχύτητες των άκρων Α και Β της ράβδου.

β) Η στροφορμή και ο ρυθμός μεταβολής της στροφορμής της ράβδου ως προς το σημείο Ο.

Δίνεται η ροπή αδράνειας μιας ομογενούς ράβδου ως προς κάθετο άξονα που περνά από το μέσον της Ι_cm= mℓ²/12 και g=10m/s².

Απάντηση:

ή

 Μια ράβδος στο άκρο νήματος

Μια ράβδος στο άκρο νήματος

Δυο ράβδοι, ένα στερεό

Έχουμε δημιουργήσει ένα επίπεδο στερεό s, καρφώνοντας δύο ομογενείς ράβδους ΑΟ και ΟΒ, κάθετα μεταξύ.  Η ράβδος ΑΟ με μήκος ℓ₁=1,6m και η ΟΒ με μήκος ℓ₂=1,2m και μάζα m=10kg. Το στερεό s στρέφεται δεξιόστροφα, γύρω από σταθερό οριζόντιο άξονα ο οποίος  διέρχεται από το μέσον Μ της ΑΟ, σε κατακόρυφο επίπεδο και κάποια στιγμή περνά από τη θέση που δείχνει το διπλανό σχήμα, όπου η ράβδος ΑΟ είναι οριζόντια. Τη στιγμή αυτή το μέσον Κ της  ράβδου ΟΒ, έχει ταχύτητα μέτρου υ_Κ=2m/s, ενώ ο ρυθμός μεταβολής του μέτρου της ταχύτητάς του είναι ίσος με 5m/s². Για τη θέση αυτή:

i)   Να σημειωθούν πάνω στο σχήμα, τα διανύσματα των ταχυτήτων και των ρυθμών μεταβολής των μέτρων τους, για τα σημεία Κ και Ο.

ii)  Να υπολογιστεί το μέτρο της ταχύτητας του κοινού άκρου Ο των δύο ράβδων, καθώς και ο ρυθμός μεταβολής του μέτρου της ταχύτητας του Ο.

iii)  Ποια η επιτάχυνση του μέσου Κ της ράβδου ΟΒ;

iv) Να βρεθεί η στροφορμή καθώς και ο ρυθμός μεταβολής της στροφορμής της ράβδου ΟΒ:

α) Ως προς το μέσον της Κ.

β) Ως προς τον άξονα περιστροφής του στερεού s, στο Μ.

iv) Να βρεθεί επίσης η στροφορμή και ο ρυθμός μεταβολής του στερεού s ως προς τον άξονα περιστροφής του.

Δίνεται η ροπή αδράνειας μιας ομογενούς ράβδου ως προς κάθετο άξονα που περνά από το μέσον της Ι_cm= mℓ²/12 και g=10m/s².

Απάντηση:

ή

  Δυο ράβδοι, ένα στερεό

Δυο ράβδοι, ένα στερεό

Δυο ράβδοι σε κίνηση

Σε λείο οριζόντιο επίπεδο ηρεμούν δυο οριζόντιες όμοιες ομογενείς ράβδοι, όπως στο διπλανό σχήμα. Οι ράβδοι μπορούν να στρέφονται χωρίς τριβές γύρω από δυο σταθερούς κατακόρυφους άξονες, όπου ο πρώτος περνά από το μέσον Κ της ράβδου ΑΒ, ενώ ο δεύτερος από το άκρο Δ της ΓΔ. Οι ράβδοι είναι παράλληλοι απέχοντας απόσταση d=2m. Θέλοντας να τους θέσουμε σε περιστροφή και να αποκτήσουν την ίδια γωνιακή ταχύτητα, ασκούμε στα άκρα τους Α και Γ κατάλληλες δυνάμεις F₁ και F₂, για ορισμένα χρονικά διαστήματα, με αποτέλεσμα κάποια στιγμή, έστω t₀=0 οι ράβδοι να βρίσκονται στις αρχικές θέσεις του σχήματος, στρεφόμενες με την γωνιακή ταχύτητα που θέλουμε, χωρίς να ασκούνται πια πάνω τους οι παραπάνω δυνάμεις. Δίνεται η ροπή αδράνειας μιας ομογενούς ράβδου ως προς κάθετο άξονα που περνά από το μέσον της Ι= Μℓ²/12.

i)   Αν το έργο της δύναμης F₁, στη διάρκεια της επιτάχυνσης της πρώτης ράβδου είναι ίσο με 4J, πόσο είναι το αντίστοιχο έργο της δύναμης F₂;

Δίνεται ότι κάθε ράβδος έχει μάζα Μ=6kg και μήκος ℓ=2m.

ii) Να βρεθεί η γωνιακή ταχύτητα που απέκτησαν οι ράβδοι.

iii) Να υπολογισθούν οι δυνάμεις που οι άξονες ασκούν στις ράβδους τη στιγμή t₀=0.

iv) Τη στιγμή t₀=0 αφαιρούνται ταυτόχρονα οι δυο άξονες  περιστροφής και οι ράβδοι κινούνται ως ελεύθερα στερεά. Να υπολογιστούν τη χρονική στιγμή t₁=2,25π s≈7 s:

α)  οι ταχύτητες των άκρων Α και Γ των δύο ράβδων,

β) η απόσταση μεταξύ των δύο αυτών άκρων.

Απάντηση:

ή

 Δυο ράβδοι σε κίνηση

Δυο ράβδοι σε κίνηση

Η επιτάχυνση και η επιβράδυνση ενός τροχού

Ένας τροχός αυτοκινήτου επιταχύνεται, μέσω άσκησης ροπής ζεύγους δυνάμεων, από τη μηχανή. Αλλά και το φρενάρισμα  επιτυγχάνεται με την άσκηση ροπής ζεύγους, μέσω των φρένων. Βέβαια και στις δύο περιπτώσεις παίζει πρωτεύοντα ρόλο και η τριβή που αναπτύσσεται, ενώ στη διαδικασία εμπλέκονται όλοι οι τροχοί και το αμάξωμα του αυτοκινήτου. Παρακάτω όμως θα μελετήσουμε τη διαδικασία, για έναν μόνο τροχό.

 Έστω λοιπόν ο τροχός του σχήματος, με μάζα 10kg και ακτίνα R=0,5m, ο οποίος ηρεμεί σε οριζόντιο δρόμο με τον οποίο εμφανίζει συντελεστές τριβής μ_s=μ=0,8.

i)   Ποια είναι η μέγιστη ροπή που μπορεί να ασκηθεί, μέσω ζεύγους δυνάμεων από τη μηχανή, ώστε ο τροχός να κυλίεται (χωρίς να ολισθήσει) κατά την επιτάχυνσή του, μέχρι να αποκτήσει ταχύτητα υ_cm=32m/s, με φορά προς τα δεξιά. Ποιος ο ελάχιστος χρόνος t₁ για την απόκτηση της παραπάνω ταχύτητας;

ii)  Στο διπλανό διάγραμμα δίνεται η ταχύτητα του αυτοκινήτου (και άρα του κέντρου μάζας του τροχού) σε συνάρτηση με το χρόνο, όπου μέχρι τη στιγμή t₁ ο τροχός επιταχύνθηκε με τη μέγιστη επιτρεπόμενη  ροπή.

Να βρεθούν:

α) Η ασκούμενη τριβή στον τροχό τις χρονικές στιγμές  ½ t₁,  t₂=8s και t₃=12s.

β) Η ροπή του ζεύγους που ασκήθηκε στον τροχό κατά το φρενάρισμα.

γ) Να γίνει η γραφική παράσταση της ασκούμενης ροπής ζεύγους, από τη στιγμή t₀=0 μέχρι τη στιγμή που σταματά το αυτοκίνητο.

Δίνεται η ροπή αδράνειας του τροχού ως προς κάθετο άξονα ο οποίος περνά από το κέντρο του Ι_cm= ½ mR² και g=10m/s².

Απάντηση:

ή

 Η επιτάχυνση και η επιβράδυνση ενός τροχού

Η επιτάχυνση και η επιβράδυνση ενός τροχού

Άλλο κέντρο δίσκου, άλλο cm.

Ένα λεπτός ομογενής δίσκος, κέντρου Ο, ακτίνας R=1m και μάζας Μ=8kg, ηρεμεί σε οριζόντιο επίπεδο, ενώ στην περιφέρειά του, στο άκρο μιας κατακόρυφης ακτίνας ΟΑ, έχει προσκολληθεί ένα σώμα Σ μάζας Μ, το οποίο θεωρούμε υλικό σημείο αμελητέων διαστάσεων. Έτσι έχουμε κατασκευάσει ένα στερεό s. Κάποια στιγμή, ασκούμε στο σώμα Σ μια οριζόντια δύναμη F μέτρου F=11Ν, όπως στο σχήμα, οπότε το στερεό μας, αρχίζει να κυλίεται. Για τη στιγμή αμέσως μόλις αρχίσει η κίνηση να βρεθούν:

i)   Η γωνιακή επιτάχυνση του στερεού.

ii)  Η επιτάχυνση του κέντρου μάζας Κ του στερεού s.

iii) Η τριβή που ασκείται στο δίσκο

iv) Η επιτάχυνση του κέντρου Ο του δίσκου.

iv) Η οριζόντια συνιστώσα της δύναμης που ασκείται στο σώμα Σ από το δίσκο.

Δίνεται ότι το cm του στερεού είναι ένα σημείο Κ, στο μέσον της ακτίνας ΟΑ, ενώ η ροπή αδράνειας του δίσκου ως προς κάθετο άξονα ο οποίος περνά από το κέντρο του Ο, δίνεται από τη σχέση Ι_ο= ½ ΜR².

Απάντηση:

ή

 Άλλο κέντρο δίσκου, άλλο cm.

Άλλο κέντρο δίσκου, άλλο cm.

Κύριος ή πρωτεύων άξονας στερεού.

 

Ο ομογενής, πολύ λεπτός, δίσκος του σχήματος, μπορεί να στρέφεται σε επαφή με λείο οριζόντιο επίπεδο, γύρω από σταθερό (πραγματικό άξονα) z, ο οποίος περνά από το κέντρο του Κ όπως στο σχήμα, με γωνιακή ταχύτητα ω .

Τότε ο δίσκος έχει στροφορμή ως προς το κέντρο μάζας Κ, με μέτρο Lz=Ιcm∙ω και με διεύθυνση του άξονα, ίδια δηλαδή με τη διεύθυνση της γωνιακής ταχύτητας ω . Μπορούμε δηλαδή να γράψουμε:

  

Κάποια στιγμή αφαιρούμε τον άξονα z (φανταστείτε ένα καρφί στο έδαφος, το οποίο βγάζουμε). Ο δίσκος θα  συνεχίσει την περιστροφή του, σαν να μην άλλαξε κάτι, απλά τώρα η περιστροφή θα πραγματοποιείται γύρω από έναν νοητό, φανταστικό, ελεύθερο άξονα z΄, ο οποίος θα έχει πάρει τη θέση του πραγματικού άξονα z.

Διαβάστε τη συνέχεια σε pdf.

ή

Κύριος ή πρωτεύον άξονας  στερεού.

Κύριος ή πρωτεύων άξονας  στερεού.

Κύριος ή πρωτεύων άξονας στερεού.

 Ο ομογενής, πολύ λεπτός, δίσκος του σχήματος, μπορεί να στρέφεται σε επαφή με λείο οριζόντιο επίπεδο, γύρω από σταθερό (πραγματικό άξονα) z, ο οποίος περνά από το κέντρο του Κ όπως στο σχήμα, με γωνιακή ταχύτητα ω .

Τότε ο δίσκος έχει στροφορμή ως προς το κέντρο μάζας Κ, με μέτρο L_z=Ι_cm∙ω και με διεύθυνση του άξονα, ίδια δηλαδή με τη διεύθυνση της γωνιακής ταχύτητας ω . Μπορούμε δηλαδή να γράψουμε:

   

Κάποια στιγμή αφαιρούμε τον άξονα z (φανταστείτε ένα καρφί στο έδαφος, το οποίο βγάζουμε). Ο δίσκος θα  συνεχίσει την περιστροφή του, σαν να μην άλλαξε κάτι, απλά τώρα η περιστροφή θα πραγματοποιείται γύρω από έναν νοητό, φανταστικό, ελεύθερο άξονα z΄, ο οποίος θα έχει πάρει τη θέση του πραγματικού άξονα z.

Διαβάστε τη συνέχεια σε pdf.

ή

Κύριος ή πρωτεύον άξονας  στερεού.

Κύριος ή πρωτεύον άξονας  στερεού.

Μια ράβδος σε λείο επίπεδο

Σε λείο οριζόντιο επίπεδο, ηρεμεί μια λεπτή ομογενής ράβδος μάζας Μ=3kg και μήκους ℓ=4m. Σε μια στιγμή t₀=0 ασκείται στο σημείο Α της ράβδου, το οποίο απέχει 0,5m από το άκρο της, μια σταθερή οριζόντια δύναμη F, μέτρου F=3Ν, με διεύθυνση κάθετη στη ράβδο. Τη χρονική στιγμή t₁=√3s η ράβδος έχει περιστραφεί κατά 90° και βρίσκεται στη θέση δεξιά στο  διπλανό σχήμα.

i)  Να υπολογιστεί η αρχική επιτάχυνση του σημείου Α, εφαρμογής της δύναμης F.

ii)  Να βρεθεί η ταχύτητα του μέσου Κ της ράβδου τη στιγμή t₁.

iii) Πόσο είναι το έργο της δύναμης F  από 0-t₁ και με ποιο ρυθμό προσφέρει ενέργεια στη ράβδο τη στιγμή t₁;

iv) Να υπολογιστεί η επιτάχυνση του σημείου Α τη στιγμή t₁.

Δίνεται η ροπή αδράνειας της ράβδου, ως προς κάθετο άξονα ο οποίος περνά από το μέσον της, Ι=Μℓ²/12.

Απάντηση:

ή

 Μια ράβδος σε λείο επίπεδο

Μια ράβδος σε λείο επίπεδο

Ισορροπία και επιτάχυνση στερεού

Ένας ομογενής δίσκος, κέντρου Ο, μάζας Μ=4kg και ακτίνας R=1m, μπορεί να στρέφεται χωρίς τριβές, γύρω από σταθερό οριζόντιο άξονα ο οποίος περνά από ένα σημείο Α της περιφέρειάς του. Στο σημείο Β, αντιδιαμετρικό σημείο του Α, έχει προσκολληθεί ένα σώμα Σ, μάζας m=4kg, το οποίο μπορούμε να θεωρήσουμε υλικό σημείο αμελητέων διαστάσεων, παίρνοντας ένα στερεό s. Το στερεό ισορροπεί με τη βοήθεια οριζόντιου νήματος ΓΒ, σε τέτοια θέση ώστε η διάμετρος ΑΒ να σχηματίζει με την κατακόρυφο γωνία θ με ημθ=0,55 και συνθ=0,84.

Δίνονται η ροπή αδράνειας του δίσκου ως προς κάθετο άξονα που περνά από το κέντρο του Ι_cm= ½ ΜR² και g=10m/s².

i)  Να υπολογιστεί η τάση του νήματος.

ii) Να βρεθεί η δύναμη που ασκεί ο άξονας στον δίσκο, στο σημείο Α.

iii) Σε μια στιγμή κόβουμε το νήμα, με αποτέλεσμα το στερεό s να αρχίσει να στρέφεται γύρω από τον άξονα, διαγράφοντας κατακόρυφο επίπεδο. Για τη στιγμή t=0, αμέσως μετά το κόψιμο του νήματος να βρεθούν:

α) Η επιτάχυνση του υλικού σημείου Σ.

β) Η δύναμη που ασκεί ο άξονας στο δίσκο.

Απάντηση:

ή

 Ισορροπία και επιτάχυνση στερεού

Ισορροπία και επιτάχυνση στερεού

Κόβοντας έναν δίσκο στη μέση

Ένας ομογενής δίσκος, κέντρου Κ, ακτίνας R και μάζας Μ, μπορεί να περιστρέφεται χωρίς τριβές, γύρω από οριζόντιο άξονα, ο οποίος περνά από ένα σημείο Α της περιφέρειάς του, με το επίπεδό του κατακόρυφο. Φέρνουμε το δίσκο στη θέση που δείχνει το διπλανό σχήμα, όπου η ακτίνα ΚΑ είναι οριζόντια και τον αφήνουμε να περιστραφεί, με αποτέλεσμα το σημείο Β, αντιδιαμετρικό του Α, να αποκτά αρχική επιτάχυνση μέτρου α₁=4g/3.

i) Η ροπή αδράνειας του δίσκου ως προς τον άξονα περιστροφής του στο Α, δίνεται από την εξίσωση:

α) Ι₁= ½ ΜR²,   β) Ι₁= ΜR²,   γ) Ι₁= 1,5ΜR²,   δ) Ι₁= 2 ΜR².

ii) Κόβουμε το δίσκο κατά μήκος της διαμέτρου ΑΒ, κρατώντας το ένα τμήμα του, το οποίο μπορεί να στρέφεται γύρω από τον ίδιο άξονα στο Α. Φέρνουμε το ημικύκλιο στη θέση του σχήματος, όπου και πάλι η διάμετρος ΑΒ να είναι οριζόντια, οπότε ο φορέας του βάρους διέρχεται ξανά από το κέντρο Κ και το αφήνουμε να περιστραφεί. Η αρχική επιτάχυνση του σημείου Κ θα έχει μέτρο:

α) α₂=g/3,   β) α₂=2g/3,    γ) α₂=g,   δ) α₂=4g/3.

όπου g η επιτάχυνση της βαρύτητας.

Να δικαιολογήσετε τις απαντήσεις σας

Απάντηση:

ή

 Κόβοντας έναν  δίσκο στη μέση

 Κόβοντας έναν  δίσκο στη μέση

Από την τετράγωνη πλάκα στην τριγωνική

Μια ομογενής τετράγωνη πλάκα μάζας Μ και πλευράς α, μπορεί να στρέφεται χωρίς τριβές γύρω από σταθερό οριζόντιο άξονα, ο οποίος διέρχεται από την κορυφή της Α. Συγκρατούμε την πλάκα, στη θέση που φαίνεται στο σχήμα, όπου η πλευρά της ΑΒ είναι οριζόντια, ενώ το επίπεδό είναι κατακόρυφο. Σε μια στιγμή η πλάκα αφήνεται να περιστραφεί, οπότε η κορυφή Β αποκτά αρχική επιτάχυνση μέτρου α_Β= 3g/4=7,5m/s².

i)  Να υπολογιστούν:

α) Η αρχική επιτάχυνση του κέντρου Κ της πλάκας.

β) η ροπή αδράνειας της πλάκας ως προς τον άξονα περιστροφής της, σε συνάρτηση με τη μάζα Μ και το μήκος της πλευράς α.

ii) Να υπολογιστεί η ροπή αδράνειας της πλάκας ως προς άξονα, κάθετο στο επίπεδο της πλάκας, ο οποίος περνά από το κέντρο Κ του τετραγώνου, αν Μ=12kg και α=1m.

 iii) Κόβουμε την τετράγωνη πλάκα κατά μήκος της διαγωνίου ΒΔ, με αποτέλεσμα να πάρουμε δύο ίσα ορθογώνια και ισοσκελή τρίγωνα. Η τριγωνική πλάκα ΑΒΔ, παραμένει στη θέση της και μπορεί να περιστρέφεται γύρω από τον οριζόντιο άξονα, που περνά από την κορυφή Α. Αφήνουμε ξανά την νέα πλάκα να περιστραφεί από την θέση του σχήματος, όπου η πλευρά ΑΒ είναι οριζόντια.

α) Να υπολογιστεί η ροπή αδράνειας της τριγωνικής πλάκας, ως προς τον άξονα περιστροφής της.

β) Ποια η αρχική επιτάχυνση της κορυφής Β και του μέσου Κ της πλευράς ΒΔ.

Δίνεται g=10m/s².

Απάντηση:

ή

 Από την τετράγωνη πλάκα στην τριγωνική

 Από την τετράγωνη πλάκα στην τριγωνική

Ένας δίσκος και ένα υλικό σημείο.

Ένας ομογενής δίσκος, κέντρου Κ, μάζας Μ=1,2kg και ακτίνας R=1m, μπορεί να στρέφεται χωρίς τριβές, γύρω από σταθερό οριζόντιο άξονα ο οποίος περνά από ένα σημείο Α της περιφέρειάς του. Ο δίσκος ισορροπεί με τη βοήθεια οριζόντιου νήματος ΓΔ, το οποίο δένεται στο άκρο μιας οριζόντιας ακτίνας ΚΓ, ενώ στη θέση Β, σε κατακόρυφη απόσταση (ΑΒ)= x=R, έχει  στερεωθεί ένα μικρό σώμα Σ, το οποίο θεωρούμε αμελητέων διαστάσεων. Έτσι έχουμε δημιουργήσει ένα στερεό s.

Δίνονται για τη  γωνία θ που σχηματίζει η ακτίνα ΚΑ με την κατακόρυφο, ημθ=0,8 και συνθ=0,6, η ροπή αδράνειας του δίσκου ως προς κάθετο άξονα που περνά από το κέντρο του Ι_cm= ½ ΜR² και g=10m/s².

i)  Να υπολογιστεί η τάση του νήματος.

ii) Σε μια στιγμή κόβουμε το νήμα, με αποτέλεσμα αμέσως μετά, το κέντρο Κ του δίσκου να αποκτήσει επιτάχυνση μέτρου 4,8m/s². Ζητούνται:

α) Να σχεδιάστε στο σχήμα τις επιταχύνσεις των σημείων Κ και Β, μόλις κοπεί το νήμα.

β) Να προσδιοριστεί η μάζα του σώματος Σ.

iii) Να υπολογιστεί η δύναμη που ασκείται στο δίσκο από τον άξονα περιστροφής, πριν το κόψιμο του νήματος.

Απάντηση:

ή

  Ένας  δίσκος και ένα υλικό σημείο.

Ένας  δίσκος και ένα υλικό σημείο.

Η ράβδος και το ζεύγος δυνάμεων.

Σε λείο οριζόντιο επίπεδο, ηρεμεί μια οριζόντια ομογενής ράβδος ΑΒ, μήκους ℓ=2m και μάζας 6kg, η οποία μπορεί να  στρέφεται γύρω από σταθερό κατακόρυφο άξονα z, ο οποίος περνά από το άκρο της Β. Στη ράβδο ασκείται ένα ζεύγος  δυνάμεων, όπως στο σχήμα και μια οριζόντια σταθερή δύναμη F,  μέτρου F=4Ν η οποία ασκείται κάθετα στη ράβδο στο σημείο Γ, όπου (ΒΓ)=0,5m.

i)  Να σχεδιαστεί η δύναμη F και να υπολογιστεί η ροπή του ζεύγους των δυνάμεων F₁ και F₂

ii)  Υποστηρίζεται η άποψη, ότι ένα στερεό στο οποίο ασκείται ένα ζεύγος δυνάμεων, δεν μπορεί να ισορροπεί με την άσκηση μιας μόνο επιπλέον δύναμης. Χρειάζεται να ασκηθεί ένα ακόμη ζεύγος δυνάμεων. Να εξετάσετε την ορθότητα ή μη της πρότασης αυτής, χρησιμοποιώντας την παραπάνω ράβδο.

iii) Να υπολογιστεί η αρχική επιτάχυνση (t=0) του άκρου Α της ράβδου, αν η δύναμη F έχει την κατεύθυνση του δεξιού σχήματος, κάθετη στη ράβδο, ενώ η ράβδος ΑΒ:

α) Μπορεί να στρέφεται γύρω από τον άξονα z, στο άκρο Β.

β) Έχει αποδεσμευτεί από τον άξονα αυτόν και είναι ελεύθερη.

Δίνεται η ροπή αδράνειας της ράβδου ως προς κάθετο άξονα ο οποίος περνά από το μέσον της Μ, Ι_cm= mℓ²/12.

Απάντηση:

ή

 Η ράβδος και το ζεύγος δυνάμεων.

 Η ράβδος και το ζεύγος δυνάμεων.

Ισορροπία κυλίνδρου σε κεκλιμένο επίπεδο.

Ένας ομογενής κύλινδρος ηρεμεί σε κεκλιμένο επίπεδο κλίσεως θ, με τη βοήθεια νήματος, το οποίο έχουμε τυλίξει γύρω του, με διεύθυνση κάθετη στο επίπεδο, όπως στο πρώτο από τα διπλανά σχήματα. Δίνεται ημθ=0,4 και συνθ≈0,9.

i)  Να αποδείξτε ότι το κεκλιμένο επίπεδο δεν είναι λείο.

ii) Να υπολογιστεί ο ελάχιστος συντελεστής οριακής στατικής τριβής, μεταξύ κυλίνδρου και επιπέδου, για την παραπάνω ισορροπία.

iii) Υποστηρίζεται ως εναλλακτική ισορροπία, αυτή του δεύτερου σχήματος. Να εξετάσετε αν είναι δυνατή η ισορροπία αυτή.

Απάντηση:

ή

 Ισορροπία κυλίνδρου σε κεκλιμένο επίπεδο.

Ισορροπία κυλίνδρου σε κεκλιμένο επίπεδο.

Ομοαξονικοί κύλινδροι σε κεκλιμένο επίπεδο…

Το στερεό του σχήματος, βάρους w, αποτελείται από δύο κολλημένους ομοαξονικούς κυλίνδρους με ακτίνες R και r= ½R  αντίστοιχα. Το στερεό ισορροπεί όπως στο σχήμα σε κεκλιμένο επίπεδο κλίσεως θ, όπου ημθ=0,6, ενώ στον δίσκο ακτίνας r έχουμε τυλίξει αβαρές μη εκτατό νήμα και στο άκρο του Α ασκούμε δύναμη F, παράλληλης στο επίπεδο.

i)  Να εξηγήσετε γιατί το κεκλιμένο επίπεδο δεν είναι λείο.

ii) Να σχεδιάστε την τριβή που ασκείται στο στερεό, δικαιολογώντας και την κατεύθυνσή της.

iii) Το μέτρο της δύναμης F είναι ίσο:

α) F=0,8w,    β) F=w,     γ) F=1,2w.  

iv) Αν για τους συντελεστές οριακής στατικής τριβής και τριβής ολίσθησης ισχύει μ=μ_s=7/8 και κάποια στιγμή αυξήσουμε το μέτρο της ασκούμενης δύναμης F στην τιμή F=1,5w, τι θα συμβεί με το στερεό:

α) Θα μετακινηθεί προς τα πάνω.

β) Θα περιστραφεί.

γ) Θα εκτελέσει σύνθετη κίνηση.

Να δικαιολογήσετε τις απαντήσεις σας.

Απάντηση:

ή

 Ομοαξονικοί κύλινδροι σε κεκλιμένο επίπεδο…

Ομοαξονικοί κύλινδροι σε κεκλιμένο επίπεδο…

Στήριξη σε δύο λεία κεκλιμένα επίπεδα.

Μια μη ομογενής ράβδος ΑΒ, μήκους ℓ και βάρους w, ισορροπεί σε επαφή με δύο λεία κεκλιμένα επίπεδα, με κλίσεις  θ=30° και φ=60°, σε οριζόντια θέση, όπως στο σχήμα. Η ροπή του βάρους της ράβδου, ως προς το κοινό σημείο Ο, της βάσης των δύο επιπέδων, έχει μέτρο:

α) τ=w∙ ¼ ℓ,       β) τ=w∙ 1/3 ℓ,       γ) τ=w∙ ½ ℓ      

Απάντηση:

ή

 Στήριξη σε δύο λεία κεκλιμένα επίπεδα.

 Στήριξη σε δύο λεία κεκλιμένα επίπεδα.