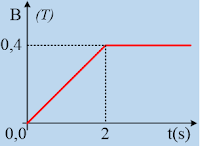
Η ράβδος ΑΓ μήκους ℓ=1m και μάζας m=0,5kg μπορεί να κινείται χωρίς τριβές, σε επαφή με τους οριζόντιους αγωγούς xx΄ και yy΄ παραμένοντας συνεχώς κάθετη σε αυτούς. Τα άκρα x και y των αγωγών συνδέονται μέσω ενός αντιστάτη με αντίσταση R=0,2Ω, ενώ η ράβδος και οι αγωγοί xx΄ και yy΄ δεν παρουσιάζουν αντίσταση. Κάποια στιγμή tο=0 στον χώρο δημιουργείται ομογενές μαγνητικό πεδίο έντασης B, με φορά όπως στο σχήμα, το μέτρο της οποίας μεταβάλλεται όπως στο δεύτερο σχήμα.
i) Για το χρονικό διάστημα από 0 έως τη στιγμή t1=2,5s, να υπολογιστούν:
α) Η απαραίτητη οριζόντια δύναμη F1 που πρέπει να ασκούμε στην ράβδο ΑΓ, ώστε να μην μετακινηθεί, παραμένοντας στην θέση της, και να κάνετε τη γραφική της παράσταση σε συνάρτηση με το χρόνο, αν δίνεται η απόσταση (xΑ)=d=0,8m.
β) Η ενέργεια που μεταφέρεται στη ράβδο μέσω της παραπάνω δύναμης F1, καθώς και το αντίστοιχο έργο της ασκούμενης, από το μαγνητικό πεδίο στη ράβδο, δύναμης Laplace.
γ) Η ηλεκτρική ενέργεια που εμφανίζεται στο κύκλωμα.
ii) Τη χρονική στιγμή t1 ασκούμε στο μέσον της ράβδου μια σταθερή οριζόντια δύναμη με φορά προς τα δεξιά, μέτρου F2=2Ν, με αποτέλεσμα μετά από λίγο, τη στιγμή t2 η ράβδος να έχει ταχύτητα υ2=2m/s. Για τη στιγμή αυτή να υπολογιστούν:
α) Ο ρυθμός με τον οποίο μεταφέρεται ενέργεια στη ράβδο, μέσω του έργου της δύναμης F2, καθώς και η αντίστοιχη ισχύς της δύναμης Laplace.
β) Η ηλεκτρική ισχύς που εμφανίζεται στο κύκλωμα, καθώς και ο ρυθμός μεταβολής της κινητικής ενέργειας της ράβδου.
ή


Δεν υπάρχουν σχόλια:
Δημοσίευση σχολίου