Μεταβάλλοντας την δύναμη στο έμβολο

Ένα κυλινδρικό δοχείο είναι γεμάτο με νερό, ενώ στην άνω βάση του υπάρχει μια μικρή τρύπα με άνοιγμα Α₁=5cm². Το ύψος του δοχείου είναι h=1m, ενώ σε απόσταση y=0,4m από την βάση του, υπάρχει άνοιγμα στο οποίο έχει συνδεθεί ένα έμβολο εμβαδού Α₂=10cm². Το έμβολο, μπορεί να κινείται χωρίς τριβές και για να παραμένει ακίνητο, του ασκούμε μια οριζόντια δύναμη F, όπως στο πρώτο σχήμα (πολλές φορές σχεδιάζουμε τη δύναμη όπως στο μεσαίο σχήμα…),

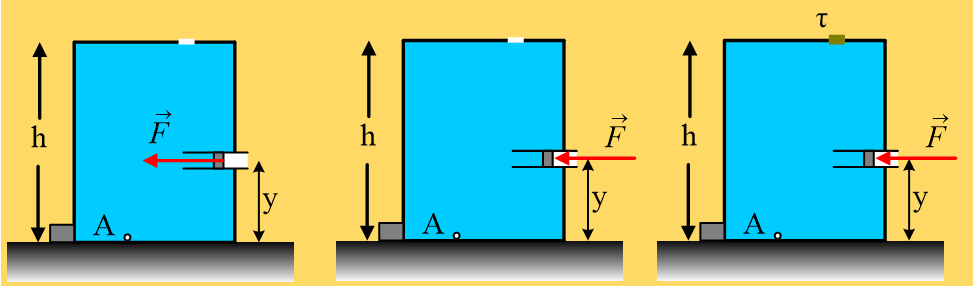
i)   Θεωρώντας το νερό ασυμπίεστο ιδανικό ρευστό και το ύψος του εμβόλου αμελητέο σε σχέση με το ύψος του δοχείου, να βρείτε το μέτρο της ασκούμενης στο έμβολο δύναμης F, καθώς και την πίεση στο σημείο Α του πυθμένα του δοχείου.

ii) Ένας συμμαθητής σας υποστηρίζει ότι αν αυξήσουμε το μέτρο της ασκούμενης δύναμης, στην σταθερή τιμή F₁=8Ν, μπορούμε να φέρουμε το έμβολο σε μια νέα θέση αριστερότερα της αρχικής, όπου να ισορροπεί. Να εξετάσετε αν αυτό είναι σωστό ή όχι.

iii) Κλείνουμε την τρύπα με μια τάπα (αμελητέου βάρους), προσέχοντας να μην παραμείνει αέρας μέσα στο δοχείο, ενώ ασκούμε διαρκώς τη δύναμη F στο έμβολο. Στη συνέχεια αφήνουμε ελεύθερο το έμβολο, παύοντας να του ασκούμε δύναμη.

α) Θα μετακινηθεί ή όχι το έμβολο από την αρχική του θέση;

β) Να υπολογιστεί η πίεση στον πυθμένα (σημείο Α) καθώς και η δύναμη που το νερό ασκεί στην τάπα.

iv) Αν η μέγιστη δύναμη στατικής τριβής μεταξύ τάπας και τοιχώματος (η οποία διατηρεί την τάπα στη θέση της) έχει μέτρο 10Ν, πόση δύναμη πρέπει να ασκήσουμε στο έμβολο, ώστε να βγάλουμε την τάπα;

Δίνεται η ατμοσφαιρική πίεση p_ατ=10⁵Ρα, η πυκνότητα του νερού ρ=1.000kg/m³ και η επιτάχυνση της βαρύτητας g=10m/s².

Απάντηση:

ή

 Μεταβάλλοντας την δύναμη στο έμβολο

Μεταβάλλοντας την δύναμη στο έμβολο