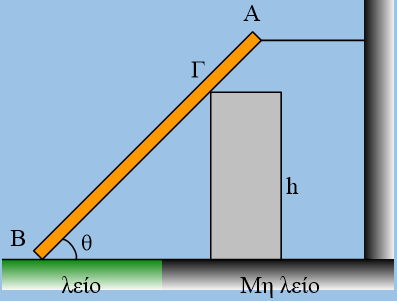
Μια ομογενής λεία ράβδος ΑΒ, μήκους ℓ=1m και βάρους w=40Ν, ισορροπεί όπως στο σχήμα, σχηματίζοντας γωνία θ με το λείο οριζόντιο επίπεδο, όπου ημθ=0,6 (συνθ=0,8), δεμένη με οριζόντιο νήμα, στο άκρο της Α. Η ράβδος στηρίζεται στην κορυφή Γ ενός βαρέος ορθογωνίου, ύψους h, το οποίο ισορροπεί σε μη λείο επίπεδο.
i) Αν h=45,6cm, να υπολογιστεί η τάση του νήματος και η δύναμη που ασκείται στη ράβδο από το οριζόντιο επίπεδο.
ii) Να βρεθεί το ελάχιστο ύψος hmin του ορθογωνίου, ώστε να μην χάνει η ράβδος την επαφή με το λείο οριζόντιο επίπεδο, διατηρώντας σταθερή την κλίση της θ με το επίπεδο, με δεδομένο ότι το ορθογώνιο παραμένει ακίνητο.
iii) Να βρεθεί η τριβή που ασκείται στο ορθογώνιο από το επίπεδο στην παραπάνω περίπτωση,
ή

Δεν υπάρχουν σχόλια:
Δημοσίευση σχολίου