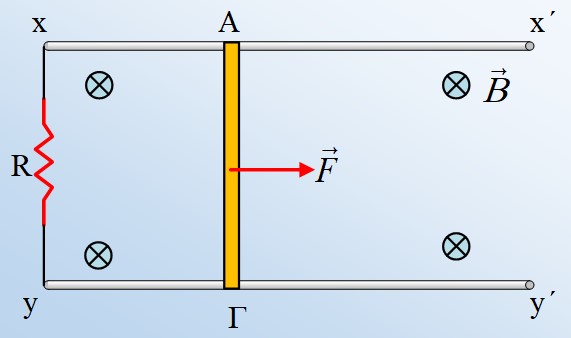
Η μεταλλική ράβδος ΑΓ, μήκους l=1m, μάζας 0,5kg και αμελητέας αντίστασης, μπορεί να κινείται οριζόντια όπως στο σχήμα, μέσα σε ένα κατακόρυφο ομογενές μαγνητικό πεδίο έντασης Β=0,5Τ, σε επαφή με δύο οριζόντιους ευθύγραμμους αγωγούς xx΄ και yy΄, οι οποίοι δεν παρουσιάζουν αντίσταση, χωρίς τριβές. Ένας αντιστάτης με αντίσταση R=2Ω, συνδέεται στα άκρα x και y των δύο αγωγών. Σε μια στιγμή t0=0, ασκούμε στην ράβδο ΑΓ μια οριζόντια δύναμη F παράλληλη προς τους αγωγούς xx΄ και yy΄, το μέτρο της οποίας μεταβάλλεται όπως στο διπλανό διάγραμμα, με αποτέλεσμα ο αγωγός να κινείται με σταθερή επιτάχυνση, μέχρι τη στιγμή t1=2s.
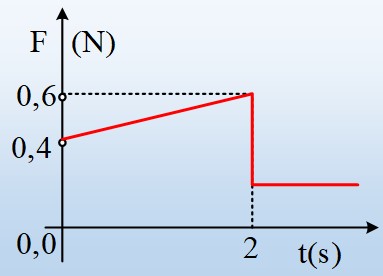
i) Να υπολογιστεί η επιτάχυνση της ράβδου ΑΓ από 0-2s.
ii) Για τη στιγμή που το μέτρο της δύναμης παίρνει την τιμή F=0,5Ν, να βρεθούν:
α) Η ΗΕΔ από επαγωγή που αναπτύσσεται πάνω στον αγωγό ΑΓ.
β) Η ηλεκτρική ισχύς που εμφανίζεται στο κύκλωμα.
γ) Η ισχύς της δύναμης F και ο ρυθμός μεταβολής της κινητικής ενέργειας της ράβδου ΑΓ.
iii) Να υπολογιστεί ο ρυθμός με τον οποίο η δύναμη F μεταφέρει ενέργεια στον ΑΓ, τη χρονική στιγμή t2=2,4s,
ή

Δεν υπάρχουν σχόλια:
Δημοσίευση σχολίου