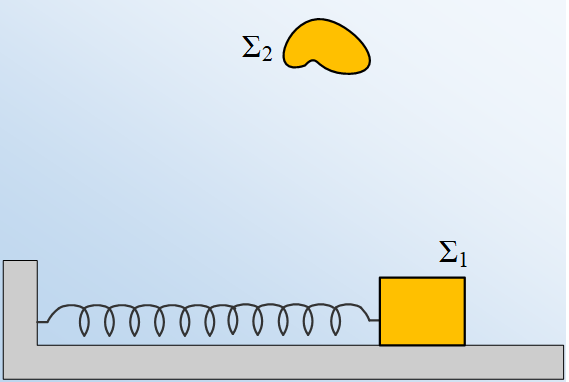
Ένα σώμα Σ1, μάζας m εκτελεί ΑΑΤ, σε λείο οριζόντιο επίπεδο, δεμένο στο άκρο ιδανικού ελατηρίου σταθεράς k, με πλάτος ταλάντωσης Α0. Κάποια στιγμή αφήνεται από ορισμένο ύψος ένα δεύτερο σώμα Σ2, μάζας Μ να πέσει, οπότε συγκρούεται πλαστικά με το σώμα Σ1 και το συσσωμάτωμα ξεκινά μια νέα ΑΑΤ, με πλάτος ταλάντωσης Α1.
i) Να γίνει η γραφική παράσταση Α12=f(υ12), όπου υ1 η ταχύτητα του Σ1, ελάχιστα πριν την κρούση.
ii) Αν Μ=3m, να υπολογιστεί το ελάχιστο πλάτος ταλάντωσης του συσσωματώματος.
iii) Αν το ποσοστό απώλειας της κινητικής ενέργειας του συστήματος κατά την παραπάνω πλαστική κρούση, που οδηγεί σε ελάχιστο πλάτος, είναι ίσο με 87,5%, να υπολογιστεί ο λόγος U2,αρχ/Ετ,1, όπου U2,αρχ η αρχική δυναμική ενέργεια του Σ2 τη στιγμή που αφήνεται να πέσει και Ετ,1 η αρχική ενέργεια ταλάντωσης του σώματος Σ1.
ή

Δεν υπάρχουν σχόλια:
Δημοσίευση σχολίου