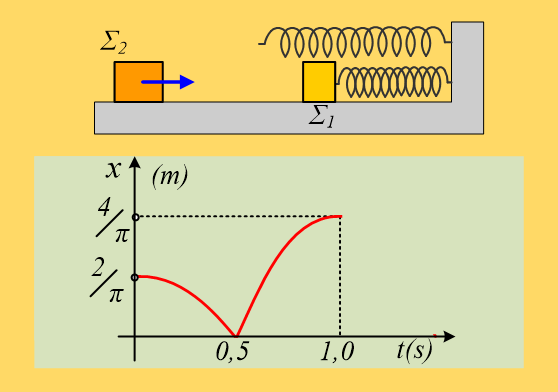
Ένα σώμα Σ1 είναι δεμένο στο άκρο ενός ιδανικού ελατηρίου σταθεράς k=2∙π2≈20Ν/m και συγκρατείται σε λείο οριζόντιο επίπεδο, έχοντας συμπιέσει το ελατήριο κατά (2/π)m. Ένα δεύτερο σώμα Σ2 κινείται στο ίδιο οριζόντιο επίπεδο, κατά μήκος του άξονα του ελατηρίου πλησιάζοντας το σώμα Σ1. Σε μια στιγμή t0=0, αφήνουμε το Σ1 να ταλαντωθεί και στο διπλανό σχήμα βλέπετε τη γραφική παράσταση της απομάκρυνσής του από τη θέση ισορροπίας του σε συνάρτηση με το χρόνο, μέχρι τη στιγμή t2=1s, όπου μηδενίζεται στιγμιαία η ταχύτητά του για πρώτη φορά, μετά την κρούση του με το σώμα Σ2.
i) Να βρεθεί η μάζα του σώματος Σ1, καθώς και η ταχύτητά του ελάχιστα πριν και αμέσως μετά την κρούση του με το σώμα Σ2.
ii) Υποστηρίζεται ότι η κρούση μεταξύ των δύο σωμάτων μπορεί να είναι πλαστική. Να εξετάσετε αν αυτό μπορεί να ισχύει.
iii) Παρακολουθώντας την παραπέρα κίνηση του σώματος Σ1, διαπιστώνουμε ότι η απομάκρυνση, από τη θέση ισορροπίας του, μεταβάλλεται συνολικά όπως στο διπλανό σχήμα. Αν οι κρούσεις μεταξύ των σωμάτων είναι ελαστικές:
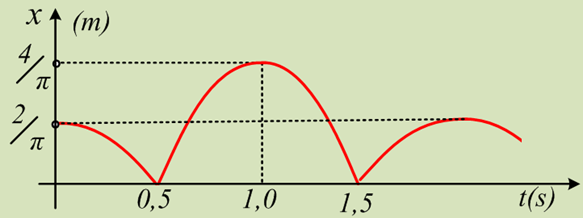
α) Ποια η κινητική ενέργεια του σώματος Σ2 πριν την πρώτη του κρούση με το Σ1 και ποια αμέσως μετά την κρούση;
ή

Δεν υπάρχουν σχόλια:
Δημοσίευση σχολίου