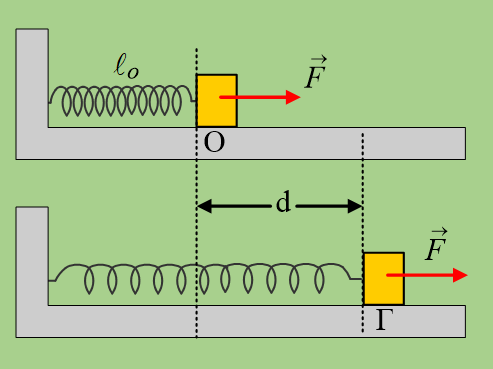
Ένα σώμα μάζας 2kg ηρεμεί σε λείο οριζόντιο επίπεδο, δεμένο στο άκρο οριζόντιου ιδανικού ελατηρίου σταθεράς k=20Ν/m, στη θέση Ο. Ασκούμε στο σώμα για t0=0, μια σταθερή οριζόντια δύναμη μέτρου F=8Ν με αποτέλεσμα να επιμηκύνεται το ελατήριο, μέχρι τη στιγμή t1 που το σώμα έχοντας μετακινηθεί κατά d=0,8m, φτάνει στη θέση Γ, όπου παύει να ασκείται πάνω του η δύναμη F.
i) Να υπολογιστεί η επιτάχυνση του σώματος:
α) στην αρχική θέση, μόλις ασκηθεί η δύναμη F,
β) όταν το ελατήριο έχει επιμήκυνση Δl1=0,4m,
γ) στην θέση Γ, πριν καταργηθεί η δύναμη F και αμέσως μετά την κατάργησή της.
ii) Να βρεθεί η μέγιστη κινητική ενέργεια του σώματος για το διάστημα που ασκείται πάνω του η δύναμη F.
iii) Πόσο χρόνο ασκήθηκε στο σώμα η δύναμη F;
iv) Να γίνει η γραφική παράσταση x=x(t) της απομάκρυνσης του σώματος από την αρχική θέση ισορροπίας του Ο, σε συνάρτηση με το χρόνο, μέχρι τη χρονική στιγμή t2= 2s.
Θεωρείστε ότι π2≈10.
ή

Δεν υπάρχουν σχόλια:
Δημοσίευση σχολίου