Ένα διάγραμμα και μια εξαναγκασμένη ταλάντωση

 

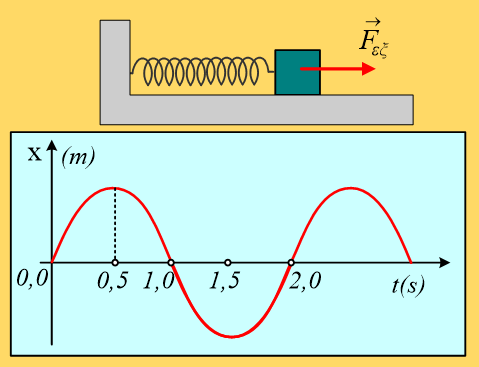
Ένα σώμα μάζας m εκτελεί εξαναγκασμένη ταλάντωση σε λείο οριζόντιο επίπεδο, δεμένο στο άκρο ιδανικού ελατηρίου σταθεράς k=40∙m (S.Ι.), με την επίδραση περιοδικής εξωτερικής δύναμης F_εξ, ενώ πάνω του δρα και δύναμη απόσβεσης της μορφής F_απ=-bυ. Στο διάγραμμα δίνεται η γραφική παράσταση της απομάκρυνσής του από τη θέση ισορροπίας του (θέση φυσικού μήκους του ελατηρίου), σε συνάρτηση με το χρόνο, όπου η προς τα δεξιά κατεύθυνση θεωρείται θετική.

i) Η ιδιοσυχνότητα ταλάντωση του σώματος είναι:

α) f₀  < 0,5Ηz,      β) f₀  = 0,5Ηz,    γ) f₀  > 0,5Ηz.

ii) Τη χρονική στιγμή t₁=0,5s, όπου το σώμα βρίσκεται σε ακραία θέση, με x=Α, η εξωτερική δύναμη F_εξ:

α) Είναι μηδενική, αφού μηδενική είναι και  η δύναμη απόσβεσης.

β) Έχει φορά προς τα δεξιά και μέτρο F_εξ= ¾ k∙Α

γ) Έχει φορά προς τα αριστερά και μέτρο F_εξ= ¼ k∙Α.

iii) Tη χρονική στιγμή t₂=1s:

α) Η δύναμη απόσβεσης έχει φορά προς τα δεξιά με μέτρο F_απ= bπA.

β) Η εξωτερική δύναμη έχει φορά προς τα αριστερά, προσφέροντας ενέργεια στο σώμα με ρυθμό:

dW/dt=  bπ²A

Να δικαιολογήσετε τις απαντήσεις σας.

Δίνεται π²≈10.

Απάντηση:

ή

 Ένα διάγραμμα και μια εξαναγκασμένη ταλάντωση

 Ένα διάγραμμα και μια εξαναγκασμένη ταλάντωση