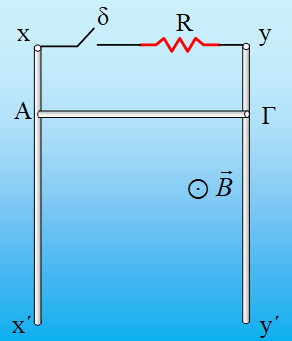
Στο διπλανό σχήμα ο αγωγός ΑΓ, μήκους 1m, μάζας 0,3kg και αντίστασης r=1Ω, μπορεί να κινείται σε επαφή με δύο κατακόρυφους αγωγούς, xx΄ και yy΄ οι οποίοι δεν εμφανίζουν αντίσταση. Μια αντίσταση R=3Ω συνδέεται μεταξύ x και y, ενώ παρεμβάλλεται ένας ανοικτός διακόπτης δ. Τη χρονική στιγμή t0=0, αφήνουμε τον αγωγό ΑΓ να κινηθεί ελεύθερα, ενώ τη στιγμή t1=0,5s κλείνουμε το διακόπτη δ. Στο χώρο υπάρχει ένα οριζόντιο μαγνητικό πεδίο έντασης Β=2Τ, κάθετο στο επίπεδο των αγωγών, όπως στο σχήμα.
i) Για τη στιγμή t1-, ελάχιστα πριν το κλείσιμο του διακόπτη δ, να υπολογιστούν η τάση VΑΓ καθώς και οι ρυθμοί μεταβολής της κινητικής και της δυναμικής ενέργειας του αγωγού.
ii) Αμέσως μετά το κλείσιμο του διακόπτη να υπολογιστούν ξανά η τάση VΑΓ καθώς και:
α) Ο ρυθμός μεταβολής της δυναμικής ενέργειας
β) Ο ρυθμός μεταβολής της κινητικής ενέργειας.
γ) Η ηλεκτρική ισχύς που εμφανίζεται στο κύκλωμα.
iii) Την ίδια στιγμή t1+ να υπολογιστεί η ισχύς κάθε δύναμης που ασκείται στον αγωγό.
iv) Αφού αποδείξετε ότι ο αγωγός ΑΓ αποκτήσει οριακή ταχύτητα (πριν φτάσει στο τέλος των κατακόρυφων αγωγών), να υπολογίσετε την τιμή της και να κάνετε ένα ποιοτικό διάγραμμα της ταχύτητας του αγωγού σε συνάρτηση με το χρόνο, από τη στιγμή t0, μέχρι την απόκτηση της οριακής ταχύτητας.
Δίνεται g=10m/s2.
ή

Δεν υπάρχουν σχόλια:
Δημοσίευση σχολίου