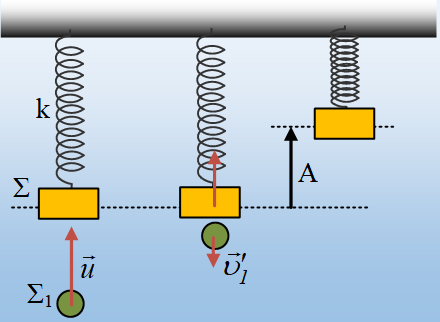
Ένα σώμα Σ μάζας Μ=2kg ηρεμεί στο κάτω άκρο κατακόρυφου ιδανικού ελατηρίου, σταθεράς k=200Ν/m, το άλλο άκρο του οποίου έχει δεθεί σε ταβάνι. Μια σφαίρα Σ1, μάζας m=1kg, κινείται κατακόρυφα με ταχύτητα u κατά μήκος του άξονα του ελατηρίου και τη στιγμή t=0, συγκρούεται με το σώμα Σ, το οποίο μετά την κρούση εκτελεί ΑΑΤ πλάτους Α=0,2m, ενώ η σφαίρα αποκτά ταχύτητα αντίθετης φοράς και μέτρου υ1΄= 0,8m/s.
i) Να υπολογιστεί η ταχύτητα u της σφαίρας πριν την κρούση.
ii) Να αποδειχθεί ότι η παραπάνω κρούση είναι ανελαστική και να υπολογιστεί η απώλεια της μηχανικής ενέργειας, στη διάρκειά της.
iii) Να βρεθούν οι συναρτήσεις της απομάκρυνσης του σώματος Σ και της δύναμης του ελατηρίου σε συνάρτηση με το χρόνο, θεωρώντας την προς τα πάνω κατεύθυνση ως θετική και να παρασταθούν γραφικά.
iv) Να υπολογιστεί η απόσταση των δύο σωμάτων, τη στιγμή που τα σώματα έχουν την ίδια επιτάχυνση, για δεύτερη φορά.
Δίνεται g=10m/s2.
ή

Δεν υπάρχουν σχόλια:
Δημοσίευση σχολίου