Ο τροχός του διπλανού σχήματος μάζας Μ=8kg και ακτίνας R=0,5m, θεωρείται ομογενής δίσκος με ροπή αδράνειας Ιcm= ½ ΜR2 και βρίσκεται ακίνητος σε οριζόντιο δρόμο.
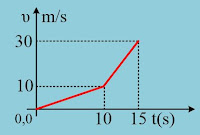
Σε μια στιγμή tο=0 ασκούνται ταυτόχρονα στον τροχό ένα ζεύγος δυνάμεων και μια οριζόντια δύναμη F, όπως στο σχήμα, με μέτρο F=4Ν. Τη στιγμή t1=10s, αλλάζουμε το μέτρο της ασκούμενης δύναμης με αποτέλεσμα η γραφική παράσταση της ταχύτητας του κέντρου Ο του τροχού, να μεταβάλλεται με το χρόνο, όπως στο διάγραμμα. Σε όλη τη διάρκεια της παραπάνω κίνησης, ο τροχός κυλίεται (χωρίς να ολισθαίνει) ενώ η ροπή του ζεύγους παραμένει σταθερή.
i) Να βρεθεί η επιτάχυνση του κέντρου Ο του τροχού καθώς και η γωνιακή του επιτάχυνση από 0-t1.
ii) Να βρεθεί η τριβή που ασκείται στον τροχό, καθώς και να υπολογιστεί η ροπή του ζεύγους, στο παραπάνω χρονικό διάστημα.
iii) Για το χρονικό διάστημα από 10s-15s, να υπολογιστούν:
α) Το μέτρο της ασκούμενης δύναμης F.
β) Η τριβή που ασκείται στον τροχό.
ή
Δεν υπάρχουν σχόλια:
Δημοσίευση σχολίου