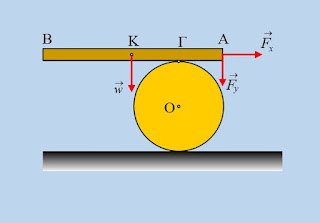
Σε οριζόντιο επίπεδο ηρεμεί ένας ομογενής κύλινδρος μάζας m=8kg, ενώ πάνω του συγκρατείται σε οριζόντια θέση μια ομογενής λεπτή δοκός ΑΒ, μήκους 4m και μάζας Μ=10kg, με τη βοήθεια μιας δύναμης που ασκείται στο άκρο της Α, με συνιστώσες Fx και Fy, όπως στο σχήμα. Η δοκός στηρίζεται στον κύλινδρο στο σημείο Γ, όπου (ΓΑ)=1m.
i) Να υπολογιστούν οι συνιστώσες Fx και Fy για την ισορροπία της δοκού.
Σε μια στιγμή t=0 μεταβάλλουμε την ασκούμενη δύναμη στο άκρο Α, καθορίζοντας σταθερή οριζόντια συνιστώσα Fx=2,6Ν. Το αποτέλεσμα είναι να τεθούν σε κίνηση και η δοκός και ο κύλινδρος, χωρίς να υπάρχει ολίσθηση ούτε μεταξύ κυλίνδρου και εδάφους, ούτε μεταξύ δοκού και κυλίνδρου.
ii) Να υπολογιστούν οι επιταχύνσεις της δοκού και του κέντρου μάζας Ο του κυλίνδρου.
iii) Να υπολογιστούν την χρονική στιγμή t1=2s :
α) Η κατακόρυφη συνιστώσα Fy της ασκούμενης δύναμης.
β) Οι κινητικές ενέργειες δοκού και κυλίνδρου.
γ) Η ισχύς της ασκούμενης δύναμης καθώς και οι ρυθμοί μεταβολής της κινητικής ενέργειας της δοκού και του κυλίνδρου.
Σε όλη τη διάρκεια της κίνησης, η δοκός παραμένει οριζόντια, g=10m/s2, ενώ η ροπή αδράνειας του κυλίνδρου ως προς τον άξονα περιστροφής του Ι= ½ mR2.
ή

Δεν υπάρχουν σχόλια:
Δημοσίευση σχολίου