Διαθέτουμε μια δεξαμενή με νερό. Για να αφαιρέσουμε μια
ποσότητα νερού από την δεξαμενή, χρησιμοποιούμε έναν ελαστικό σωλήνα σταθερής
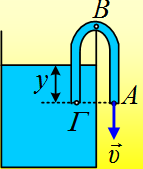
διατομής Α=2cm2, τον οποίο αφού λυγίσουμε, βυθίζουμε το ένα άκρο του
Γ κατά y=45cm στο νερό. Με αναρρόφηση στο άλλο άκρο Α, το οποίο βρίσκεται στο
ίδιο οριζόντιο επίπεδο με το Γ, πετυχαίνουμε την εκροή του νερού.
i)
Να
βρεθεί σε πόσο χρονικό διάστημα μπορούμε να γεμίσουμε ένα δοχείο όγκου 12L, θεωρώντας
ότι το εμβαδόν της επιφάνειας της δεξαμενής, είναι πολύ μεγαλύτερο από το εμβαδόν
της διατομής του σωλήνα.
ii)
Να υπολογιστεί η πίεση στο άκρο Γ και στο ανώτερο σημείο Β του σωλήνα, το οποίο
απέχει απόσταση h=1m από το επίπεδο ΑΓ.
iii)
Προκειμένου να συντομευτεί το απαιτούμενο χρονικό διάστημα άντλησης του νερού,
προτείνεται να χρησιμοποιήσουμε μακρύτερο σωλήνα, σε δυο διαφορετικά
ενδεχόμενα. Στο πρώτο, το βυθιζόμενο τμήμα του σωλήνα είναι 2y, στον
δεύτερο το άκρο Α βρίσκεται κατά y
χαμηλότερα του Γ, όπως στα σχήματα.
Ποιον τρόπο θα επιλέγατε
και γιατί; Να βρεθεί η πίεση στο άκρο Γ του σωλήνα και για τις δύο αυτές
περιπτώσεις.
Δίνεται η πυκνότητα του νερού ρ=1.000kg/m3,
η επιτάχυνση της βαρύτητας g=10m/s2 και η ατμοσφαιρική πίεση pατ=105Ν/m2,
ενώ το νερό, να θεωρηθεί ιδανικό ρευστό και όλες οι ροές μόνιμες και στρωτές.
ή


Δεν υπάρχουν σχόλια:
Δημοσίευση σχολίου