Άλλη μια πτώση πλαισίου σε μαγνητικό πεδίο

Ένα ορθογώνιο πλαίσιο αφήνεται να πέσει από ορισμένο ύψος, με το επίπεδό του κατακόρυφο και την πλευρά ΑΒ οριζόντια. Σε μια στιγμή συναντά στην πορεία του ένα ομογενές οριζόντιο μαγνητικό πεδίο, με δυναμικές γραμμές κάθετες στο πλαίσιο, και στο σχήμα φαίνεται η θέση του πλαισίου κάποια στιγμή, όπου η ταχύτητά του είναι ίση με 4m/s. Τη στιγμή αυτή στο πλαίσιο παράγεται θερμότητα με ρυθμό dQ/dt= 0,8 J/s.

i)  Δυο μαθητές διαφωνούν, στο ερώτημα για το ρυθμό μεταβολής της μαγνητικής ροής που διέρχεται από το πλαίσιο την παραπάνω στιγμή. Ο Αντώνης (Α) υποστηρίζει ότι είναι θετικός, ενώ ο Βασίλης (Β) ότι είναι αρνητικός. Ποιος έχει δίκιο;

ii) Να σχεδιάσετε στο σχήμα την ένταση του ρεύματος που διαρρέει το πλαίσιο στη θέση αυτή, δικαιολογώντας την φορά της.

iii)  Να αποδείξετε ότι το πλαίσιο δέχεται κατακόρυφη δύναμη από το μαγνητικό πεδίο, της οποίας να βρείτε  τα χαρακτηριστικά της.

iv) Αν το πλαίσιο παρουσιάζει αντίσταση R=0,2Ω, να υπολογιστεί η ΗΕΔ που αναπτύσσεται στο πλαίσιο στην θέση αυτή.

Απάντηση:

ή
 Άλλη μια πτώση πλαισίου σε μαγνητικό πεδίο

 Άλλη μια πτώση πλαισίου σε μαγνητικό πεδίο

Όχι δεν θέλουμε κίνηση πλαισίου

 Ο αγωγός ΚΛ μήκους ℓ=1m, μπορεί να κινείται οριζόντια, με σταθερή ταχύτητα υ=2m/s, με την επίδραση κατάλληλης οριζόντιας δύναμης F, σε επαφή με δυο παράλληλους αγωγούς ΑA₁ και ΓΓ₁ χωρίς τριβές. Κάποια στιγμή, την οποία θεωρούμε ως t=0, ο αγωγός ΚΛ εισέρχεται σε μια περιοχή πλάτους d=0,4m, στην οποία υπάρχει ένα κατακόρυφο ομογενές μαγνητικό πεδίο έντασης Β₁=0,5Τ, με φορά προς τα κάτω,  όπως στο σχήμα. Συνεχίζει σε μια περιοχή πλάτους επίσης d, στην οποία δεν υπάρχει μαγνητικό πεδίο για να φτάσει σε ένα δεύτερο ομογενές μαγνητικό πεδίο, του ίδιου πλάτους με ένταση Β₂=0,5Τ, αντίθετης κατεύθυνσης από το προηγούμενο. Ο αγωγός ΚΛ και οι δύο αγωγοί ΑA₁ και ΓΓ₁ δεν παρουσιάζουν αντίσταση, ενώ μεταξύ των άκρων Α και Γ συνδέεται αντιστάτης με αντίσταση R=0,5Ω.

Θεωρώντας την κάθετη στην επιφάνεια που ορίζουν οι αγωγοί να έχει φορά προς τα κάτω, ίδια με την ένταση Β₁, να βρεθούν οι συναρτήσεις και να γίνουν οι γραφικές παραστάσεις  σε συνάρτηση με το χρόνο:

i) της μαγνητικής ροής που διέρχεται από το ορθογώνιο ΑΚΛΓ.

ii) Της ΗΕΔ που αναπτύσσεται πάνω στον κινούμενο αγωγό ΚΛ.

iii) Της έντασης του ρεύματος που διαρρέει τον αντιστάτη.

iv) Της δύναμης Laplace που ασκείται στον ΚΛ

v) Της απαραίτητης δύναμης F για την παραπάνω κίνηση της ράβδου.

Απάντηση:

ή

 Όχι δεν θέλουμε κίνηση πλαισίου

 Όχι δεν θέλουμε κίνηση πλαισίου

Μελέτη μιας σύνθεσης από ένα διάγραμμα

Ένα σώμα μάζας m=0,2kg κινείται ευθύγραμμα κατά μήκος ενός προσανατολισμένου άξονα, εκτελώντας μια παλινδρομική κίνηση γύρω από την θέση x=0 και στο διάγραμμα δίνεται η θέση του σε συνάρτηση με το χρόνο, όπου οι χρονικές στιγμές που έχουν σημειωθεί στο σχήμα είναι t₁=3,74s και t₂=8,74s.

Η παραπάνω κίνηση μπορεί να θεωρηθεί ως επαλληλία δύο αρμονικών ταλαντώσεων με εξισώσεις:

x₁=2∙ημ(2πt)  και  x₂=Α₂ ∙ημ(ω₂t+ π/2)   (μονάδες στο S.Ι.)

i)  Να υπολογιστεί το πλάτος Α₂.

ii) Να βρεθεί η εξίσωση x=x(t) για την απομάκρυνση του σώματος σε συνάρτηση με το χρόνο και να υπολογιστεί η περίοδος του διακροτήματος καθώς και η γωνιακή συχνότητα ω₂.

iii) Για τη χρονική στιγμή t₃=5s να υπολογισθούν:

 α) Η ταχύτητα του σώματος.

 β) Η (συνισταμένη) δύναμη που επιταχύνει το σώμα, καθώς και η ισχύς της.

Απάντηση:

ή

 Μελέτη μιας σύνθεσης από ένα διάγραμμα

 Μελέτη μιας σύνθεσης από ένα διάγραμμα 

Ερωτήματα πάνω σε μια εξαναγκασμένη ταλάντωση

 

Ένα σώμα εκτελεί μια εξαναγκασμένη ταλάντωση δεμένο στο άκρο ιδανικού ελατηρίου, σταθεράς k, με την επίδραση εξωτερικής δύναμης F_εξ, ενώ πάνω του ασκείται και δύναμη απόσβεσης της μορφής F_απ= - b∙υ. Η εξίσωση της απομάκρυνσης του σώματος είναι x=Α∙ημ(ωt), με ω ≠ ω₀.

Να χαρακτηρίσετε τις παρακάτω προτάσεις ως σωστές ή λανθασμένες, δικαιολογώντας την θέση σας.

i)   Τη στιγμή που το σώμα βρίσκεται στο σημείο Β με απομάκρυνση x=-Α, δεν δέχεται δύναμη απόσβεσης, με αποτέλεσμα η μοναδική οριζόντια δύναμη που ασκείται στο σώμα να είναι η δύναμη του ελατηρίου.

ii) Τη στιγμή που το σώμα περνά από τη θέση ισορροπίας του (x=0), κινούμενο προς τα δεξιά, δέχεται εξωτερική δύναμη με φορά προς τα δεξιά και μέτρο F_εξ=b∙ωΑ.

iii) Κατά την κίνηση από το Β στο Ο, υπάρχει μια θέση Γ στην οποία ισχύει F_εξ=mα, όπου α η επιτάχυνση του σώματος.

Απάντηση:

ή

  Ερωτήματα πάνω σε μια εξαναγκασμένη ταλάντωση

  Ερωτήματα πάνω σε μια εξαναγκασμένη ταλάντωση

Ένα διάγραμμα και μια εξαναγκασμένη ταλάντωση

 

Ένα σώμα μάζας m εκτελεί εξαναγκασμένη ταλάντωση σε λείο οριζόντιο επίπεδο, δεμένο στο άκρο ιδανικού ελατηρίου σταθεράς k=40∙m (S.Ι.), με την επίδραση περιοδικής εξωτερικής δύναμης F_εξ, ενώ πάνω του δρα και δύναμη απόσβεσης της μορφής F_απ=-bυ. Στο διάγραμμα δίνεται η γραφική παράσταση της απομάκρυνσής του από τη θέση ισορροπίας του (θέση φυσικού μήκους του ελατηρίου), σε συνάρτηση με το χρόνο, όπου η προς τα δεξιά κατεύθυνση θεωρείται θετική.

i) Η ιδιοσυχνότητα ταλάντωση του σώματος είναι:

α) f₀  < 0,5Ηz,      β) f₀  = 0,5Ηz,    γ) f₀  > 0,5Ηz.

ii) Τη χρονική στιγμή t₁=0,5s, όπου το σώμα βρίσκεται σε ακραία θέση, με x=Α, η εξωτερική δύναμη F_εξ:

α) Είναι μηδενική, αφού μηδενική είναι και  η δύναμη απόσβεσης.

β) Έχει φορά προς τα δεξιά και μέτρο F_εξ= ¾ k∙Α

γ) Έχει φορά προς τα αριστερά και μέτρο F_εξ= ¼ k∙Α.

iii) Tη χρονική στιγμή t₂=1s:

α) Η δύναμη απόσβεσης έχει φορά προς τα δεξιά με μέτρο F_απ= bπA.

β) Η εξωτερική δύναμη έχει φορά προς τα αριστερά, προσφέροντας ενέργεια στο σώμα με ρυθμό:

dW/dt=  bπ²A

Να δικαιολογήσετε τις απαντήσεις σας.

Δίνεται π²≈10.

Απάντηση:

ή

 Ένα διάγραμμα και μια εξαναγκασμένη ταλάντωση

 Ένα διάγραμμα και μια εξαναγκασμένη ταλάντωση

Η ενέργεια και άλλα τινά σε μια φθίνουσα ταλάντωση

 

Μια πλάκα μάζας m εκτελεί φθίνουσα ταλάντωση, με την επίδραση δύναμης απόσβεσης της μορφής F=-bυ, στο άκρο ενός κατακόρυφου ιδανικού ελατηρίου, σταθεράς k. Στο διάγραμμα δίνεται η απομάκρυνσή της σε συνάρτηση με το χρόνο, όπου έχουμε πάρει θετική την προς τα πάνω κατεύθυνση. Να χαρακτηρίσετε τις παρακάτω προτάσεις ως σωστές ή λανθασμένες δίνοντας και σύντομες δικαιολογήσεις.

i)  Τη στιγμή t₂ που αντιστοιχεί σε μέγιστη (τοπικά) απομάκρυνση:

α) η ενέργεια ταλάντωσης εμφανίζεται μόνο ως δυναμική.

β) Η επιτάχυνση έχει φορά προς τη θέση ισορροπίας και μέτρο ανεξάρτητο της σταθεράς απόσβεσης b.

ii) Η κινητική ενέργεια του σώματος τη στιγμή t₄ είναι ίση με τη δυναμική ενέργεια τη στιγμή t₂.

iii) Η επιτάχυνση της πλάκας τη στιγμή t₄ είναι μηδενική.

iv) Τις χρονικές στιγμές t₁ και t₃:

 α) Η πλάκα έχει ταχύτητες, με ίσα μέτρα.

 β) Η πλάκα έχει επιταχύνσεις ίσων μέτρων.

Απάντηση:

ή

 Η ενέργεια και άλλα τινά σε μια φθίνουσα ταλάντωση

 Η ενέργεια και άλλα τινά σε μια φθίνουσα ταλάντωση

Τμήματα δύο ΑΑΤ, μια ταλάντωση.

 Το σώμα του σχήματος ηρεμεί σε λείο οριζόντιο επίπεδο, δεμένο στο άκρο οριζόντιου ιδανικού ελατηρίου σταθεράς k₁ και σε επαφή (χωρίς να είναι δεμένο) με δεύτερο οριζόντιο ιδανικό ελατήριο σταθεράς k₂. Τα ελατήρια στη θέση αυτή έχουν τα φυσικά μήκη τους. Εκτρέπουμε το σώμα προς τα δεξιά συσπειρώνοντας το πρώτο ελατήριο κατά d₁ και το αφήνουμε να κινηθεί. Αν d₂ η μέγιστη συσπείρωση του ελατηρίου σταθεράς k2, όπου d₁=2d₂, τότε:

i) Μεταξύ των σταθερών των ελατηρίων ισχύει:

α) k₂= k₁,   β) k₂= 2k₁,   γ) k₂= 3k₁,   δ) k₂=4k₁.

ii) Αν Τ₁ η περίοδος της ταλάντωσης που θα εκτελούσε το σώμα αυτό στο άκρο του ελατηρίου σταθεράς k₁, τότε η περίοδος της παραπάνω κίνησης είναι ίση:

α) Τ_κ= ¼ Τ₁,    β) Τ_κ= ½ Τ₁,    α) Τ_κ= ¾ Τ₁,    α) Τ_κ=  Τ₁.

Να δικαιολογήσετε τις απαντήσεις σας.

Απάντηση:

ή

 Τμήματα δύο ΑΑΤ, μια ταλάντωση.

 Τμήματα δύο ΑΑΤ, μια ταλάντωση.

Μηχανική ενέργεια και ενέργεια ταλάντωσης

 

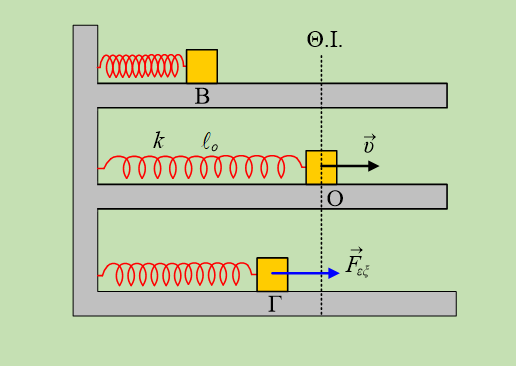
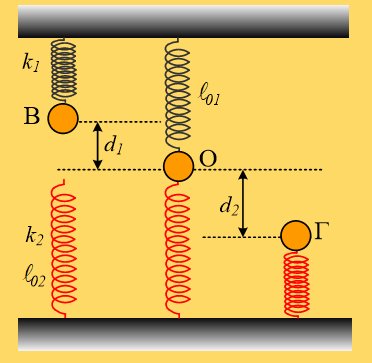
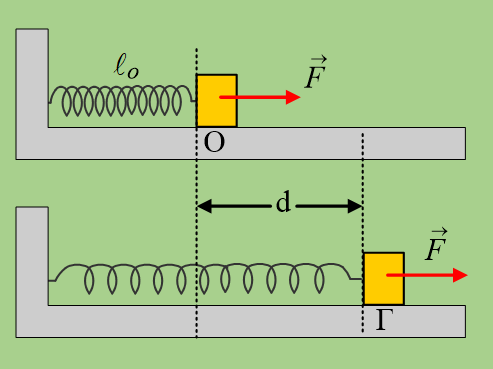
Ένα σώμα μάζας 2kg είναι δεμένο στο κάτω άκρο ενός κατακόρυφου ιδανικού ελατηρίου σταθεράς k₁=100Ν/m, το άλλο άκρο του οποίου έχει προσδεθεί στο ταβάνι και συγκρατείται στη θέση Β, έχοντας συσπειρώσει το ελατήριο κατά d₁=0,2m. Στην ίδια κατακόρυφο βρίσκεται ένα δεύτερο κατακόρυφο ιδανικό ελατήριο, σταθεράς k₂, το οποίο στηρίζεται στο έδαφος και το οποίο έχει το φυσικό μήκος του ℓ_ο=1m. Κάποια στιγμή αφήνουμε το σώμα  να κινηθεί και τη στιγμή που έρχεται σε επαφή με το δεύτερο ελατήριο, αποδεσμεύεται από το πρώτο ελατήριο, το οποίο έχει το φυσικό μήκος του και συνεχίζει  την κίνησή του, οπότε μηδενίζεται στιγμιαία η ταχύτητά του στη θέση Γ, όπου έχει συσπειρώσει το ελατήριο κατά d₂=0,5m.

i)  Να υπολογισθεί η κινητική ενέργεια του σώματος τη στιγμή που αποδεσμεύεται από το πάνω ελατήριο.

ii)  Να βρεθεί η σταθερά k₂ του δεύτερου ελατηρίου καθώς και η μέγιστη δυναμική του ενέργεια.

iii) Να υπολογιστεί η μηχανική ενέργεια του συστήματος (σώμα και δύο ελατήρια) στις θέσεις Β, Ο και Γ.

iv) Πόση είναι η ενέργεια ταλάντωσης:

α) Για την ταλάντωση από το Β στο Ο.

β) Για την ταλάντωση από το Ο στο Γ.

Θεωρείστε ως δεδομένο ότι η κίνηση του σώματος στο άκρο ενός ελατηρίου είναι ΑΑΤ, ενώ το δάπεδο λαμβάνεται ως επίπεδο μηδενικής ενέργειας και g=10m/s².

Απάντηση:

ή

Μηχανική ενέργεια και ενέργεια ταλάντωσης

Μηχανική ενέργεια και ενέργεια ταλάντωσης

Η τάση του νήματος στη διάρκεια της ταλάντωσης

 

Μια σφαίρα μάζας m ηρεμεί στο κάτω άκρο Ο ιδανικού ελατηρίου, σταθεράς k και αμελητέας μάζας, το πάνω άκρο του οποίου έχει δεθεί σε σώμα Σ μάζας Μ, που κρέμεται μέσω νήματος από το ταβάνι, όπως στο σχήμα.

i)  Η τάση του νήματος έχει μέτρο:

α) Τ_ο=Μg,  β) Τ_ο=(Μ+m)g,   γ) Τ_ο=(Μ-m)g.

ii) Ασκώντας μια κατάλληλη δύναμη  στη σφαίρα, την μετατοπίζουμε κατακόρυφα προς τα κάτω κατά d, συγκρατώντας την στη θέση Κ. Αφήνουμε τη σφαίρα να ταλαντωθεί, οπότε η ελάχιστη τιμή του μέτρου της τάσης του νήματος παίρνει τιμή Τ_min=Μg.

α) Τη στιγμή που ελαχιστοποιείται η τάση του νήματος, η επιτάχυνση της σφαίρας έχει μέτρο:

a) α₁ < g,        b)  α₁ = g,       c)  α₁ >  g.

Όπου g η επιτάχυνση της βαρύτητας.

β) Τη στιγμή που αφήνουμε τη σφαίρα στη θέση Κ να κινηθεί, η τάση του νήματος, έχει τιμή:

a)  Τ₁= 2T_o       b) Τ₁= T_o +mg,         c) Τ₁= T_o +Mg

Απάντηση:

ή

 Η τάση του νήματος στη διάρκεια της ταλάντωσης

 Η τάση του νήματος στη διάρκεια της ταλάντωσης

Η μέγιστη ενέργεια ταλάντωσης

 

Ένα σώμα Σ₁ μάζας m₁=2kg είναι δεμένο στο άκρο οριζόντιου ιδανικού ελατηρίου σταθεράς k=200Ν/m και ηρεμεί σε λείο οριζόντιο επίπεδο. Ένα δεύτερο σώμα Σ₂ μάζας m₂=0,5kg κινείται με ταχύτητα μέτρου υ₂=8m/s κατά μήκος του άξονα του ελατηρίου, πλησιάζοντας το σώμα Σ₁. Μετακινούμε το Σ₁ συμπιέζοντας το ελατήριο κατά Δℓ=0,5m, φέρνοντάς το στη θέση Γ. Σε μια στιγμή t₀=0, όπου τα δυο σώματα απέχουν κατά (ΓΔ)=D,  αφήνουμε ελεύθερο το Σ₁ να εκτελέσει ΑΑΤ, με αποτέλεσμα τα σώματα να συγκρούονται κεντρικά και ελαστικά τη χρονική στιγμή t₁=0,314s.

i)  Να υπολογιστεί η απόσταση D.

ii) Να υπολογιστεί η ενέργεια ταλάντωσης του Σ₁ αμέσως μετά την κρούση, καθώς και η ταχύτητα με την οποία φτάνει στην αρχική του θέση Γ.

ii) Επαναλαμβάνουμε τη διαδικασία, αλλά τώρα αφήνουμε το Σ₁ να κινηθεί όταν έχουμε διαφορετική απόσταση μεταξύ των σωμάτων, με αποτέλεσμα το Σ₁ να αποκτήσει τη μέγιστη δυνατή ενέργεια ταλάντωσης, μετά την κρούση.

α) Να βρεθεί η μέγιστη αυτή ενέργεια ταλάντωσης του Σ₁.

β) Να βρεθεί η θέση της κρούσης, καθώς και η ταχύτητα του Σ₁ ελάχιστα πριν την κρούση.

Απάντηση:

ή

Η μέγιστη ενέργεια ταλάντωσης

Η μέγιστη ενέργεια  ταλάντωσης

Δυο διαδοχικές ταλαντώσεις

 

Ένα σώμα μάζας 2kg ηρεμεί σε λείο οριζόντιο επίπεδο, δεμένο στο άκρο οριζόντιου ιδανικού ελατηρίου σταθεράς k=20Ν/m, στη θέση Ο. Ασκούμε στο σώμα για t₀=0, μια σταθερή οριζόντια δύναμη μέτρου F=8Ν με αποτέλεσμα να επιμηκύνεται το ελατήριο, μέχρι τη στιγμή t₁ που το σώμα έχοντας μετακινηθεί κατά d=0,8m, φτάνει στη θέση Γ, όπου παύει να ασκείται πάνω του η δύναμη F.

i) Να υπολογιστεί η επιτάχυνση του σώματος:

α) στην αρχική θέση, μόλις ασκηθεί η δύναμη F, 

β) όταν το ελατήριο έχει επιμήκυνση Δl₁=0,4m, 

γ) στην θέση Γ, πριν καταργηθεί η δύναμη F και αμέσως μετά την κατάργησή της.

ii) Να βρεθεί η μέγιστη κινητική ενέργεια του σώματος για το διάστημα που ασκείται πάνω του η δύναμη F.

iii) Πόσο χρόνο ασκήθηκε στο σώμα η δύναμη F;

iv) Να γίνει η γραφική παράσταση x=x(t) της απομάκρυνσης του σώματος από την αρχική θέση ισορροπίας του Ο, σε συνάρτηση με το χρόνο, μέχρι τη χρονική στιγμή t₂= 2s.

Θεωρείστε ότι π²≈10.

Απάντηση:

ή

Δυο διαδοχικές ταλαντώσεις

Δυο διαδοχικές ταλαντώσεις

Το διάγραμμα απομάκρυνσης και δυο κρούσεις.

 

Ένα σώμα Σ₁ είναι δεμένο στο άκρο ενός ιδανικού ελατηρίου σταθεράς k=2∙π²≈20Ν/m και συγκρατείται σε λείο οριζόντιο επίπεδο, έχοντας συμπιέσει το ελατήριο κατά (2/π)m. Ένα δεύτερο σώμα Σ₂ κινείται στο ίδιο οριζόντιο επίπεδο, κατά μήκος του άξονα του ελατηρίου πλησιάζοντας το σώμα Σ₁. Σε μια στιγμή t₀=0, αφήνουμε το Σ₁ να ταλαντωθεί και στο διπλανό σχήμα βλέπετε τη γραφική παράσταση της απομάκρυνσής του από τη θέση ισορροπίας του σε συνάρτηση με το χρόνο, μέχρι τη στιγμή t₂=1s, όπου μηδενίζεται στιγμιαία η ταχύτητά του για πρώτη φορά, μετά την κρούση του με το σώμα Σ₂.

i)  Να βρεθεί η μάζα του σώματος Σ₁, καθώς και η ταχύτητά του ελάχιστα πριν και αμέσως μετά την κρούση του με το σώμα Σ₂.

ii) Υποστηρίζεται ότι η κρούση μεταξύ των δύο σωμάτων μπορεί να είναι πλαστική. Να εξετάσετε αν αυτό μπορεί να ισχύει.

iii) Παρακολουθώντας την παραπέρα κίνηση του σώματος Σ₁, διαπιστώνουμε ότι η απομάκρυνση, από τη θέση ισορροπίας του, μεταβάλλεται συνολικά όπως στο διπλανό σχήμα. Αν οι κρούσεις μεταξύ των σωμάτων είναι ελαστικές:

 

α) Ποια η κινητική ενέργεια του σώματος Σ₂ πριν την πρώτη του κρούση με το Σ₁ και ποια αμέσως μετά την κρούση;

β) Να υπολογιστεί η μάζα του σώματος Σ₂ και η τελική του ταχύτητα.

Απάντηση:

ή

 Το  διάγραμμα απομάκρυνσης και δυο κρούσεις.

 Το  διάγραμμα απομάκρυνσης και δυο κρούσεις.

Ένας … καλός μετασχηματιστής!

 

Έστω ένας μετασχηματιστής, που οι μόνες απώλειες που παρουσιάζει είναι οι αντιστάσεις r₁=5Ω και r₂=1Ω στα δύο πηνία, όπου στο πρωτεύον έχουμε 1.000 και στο δευτερεύον 200 σπείρες. Τροφοδοτούμε το πρωτεύον με Ε.Τ. ενεργού τιμής V₁=31V και θέτουμε στο δευτερεύον αντιστάτη με R=5Ω. Οι απώλειες στον πυρήνα θεωρούνται αμελητέες. Να βρεθούν:

i) Οι ενεργές εντάσεις πρωτεύοντος δευτερεύοντος

ii) Η απόδοση του μετασχηματιστή.

Απάντηση:

ή

Ένας … καλός μετασχηματιστής!

Μια κρούση και πληροφορίες από ένα διάγραμμα

 

Σε λείο οριζόντιο επίπεδο κινούνται δυο ελαστικές σφαίρες με ίσες ακτίνες, η μία προς την άλλη, με ταχύτητες ίσου μέτρου, όπως στο σχήμα. Σε μια στιγμή συγκρούονται κεντρικά και ελαστικά και στο διάγραμμα φαίνεται η ταχύτητα της Α σφαίρας, η οποία έχει μάζα m₁=2kg, σε συνάρτηση με το χρόνο.

i)  Τι ποσοστό της αρχικής κινητικής ενέργειας της Α σφαίρας μεταφέρεται στην Β σφαίρα, στη διάρκεια της κρούσης;

ii)  Αφού υπολογίσετε την μάζα της Β σφαίρας, να χαράξετε ένα ποιοτικό διάγραμμα για την ταχύτητα της Β σφαίρας σε συνάρτηση με το χρόνο.

iii) Να υπολογιστεί η ταχύτητα της Β σφαίρας τη στιγμή t₁ που μηδενίζεται η ταχύτητα της σφαίρας Α.

iv) Πόση είναι η δυναμική ενέργεια ελαστικής παραμόρφωσης των σφαιρών τη στιγμή t₁;

v) Ένας μαθητής κοιτάζοντας το διάγραμμα που δίνεται, συμπεραίνει ότι τη στιγμή t₁ η γραφική παράσταση τέμνει σχεδόν κάθετα τον άξονα του χρόνου. Συμφωνείτε ή όχι με την εκτίμηση αυτή; Να δικαιολογήσετε την άποψή σας.

Απάντηση:

ή

 Μια κρούση και πληροφορίες από ένα διάγραμμα

 Μια κρούση και πληροφορίες από ένα διάγραμμα

Ισορροπίες με τριβές και κρούση.

Πάνω σε ένα μη λείο οριζόντιο επίπεδο, ηρεμεί ένα σώμα Σ₁ μάζας m₁=2kg, δεμένο στο άκρο οριζόντιου ιδανικού ελατηρίου σταθεράς k=20Ν/m, το οποίο έχει επιμηκύνει κατά x₁=0,2m. Ένα δεύτερο σώμα Σ₂ μάζας m₂=1kg κινείται κατά μήκος του άξονα του ελατηρίου με κατεύθυνση προς το σώμα Σ₁, με το οποίο μετά από λίγο συγκρούεται μετωπικά και ελαστικά. Τα δυο σώματα παρουσιάζουν τον ίδιο συντελεστή τριβής ολίσθησης με το επίπεδο μ=0,65. Μετά την κρούση το Σ₁ διανύει απόσταση (ΑΒ)= s=0,6m, μέχρι να μηδενιστεί η ταχύτητά του, στη θέση Β.

i)  Να υπολογιστεί η τριβή που ασκείται στο σώμα Σ₁, στη θέση Α, πριν την κρούση.

ii)  Να βρεθεί η ταχύτητα την οποία αποκτά το σώμα Σ₁, αμέσως μετά την κρούση, καθώς και η αντίστοιχη επιτάχυνσή του.

iii) Τι ποσοστό της κινητικής ενέργειας του Σ₂ ελάχιστα πριν την κρούση, μεταφέρεται στο σώμα Σ₁;

iv) Να βρεθεί η τελική απόσταση μεταξύ των δύο σωμάτων, μετά την ακινητοποίησή τους.

Δίνεται g=10m/s².

Απάντηση:

ή

Ισορροπίες με τριβές και κρούση.

Ισορροπίες με τριβές και κρούση.

Δύο κρούσεις, ένας έλεγχος

Στη θέση Ο, σε  ορισμένο ύψος από το έδαφος, συγκρατούμε δυο σφαίρες Α και Β με μάζες m₁=1kg και m₂=2kg. Σε μια στιγμή αφήνουμε την Β να πέσει και μετά από λίγο αφήνουμε την Α. Η σφαίρα Β συγκρούεται με το έδαφος και επιστρέφοντας συγκρούεται κεντρικά και ελαστικά με την Α, η οποία κατέρχεται, έχοντας τη στιγμή της κρούσης ταχύτητα μέτρου υ₁=3m/s. Μετά την κρούση η σφαίρα Α επιστρέφει στο σημείο Ο με μηδενική ταχύτητα.

i)   Να υπολογιστεί η κατακόρυφη απόσταση y μεταξύ της αρχικής θέσης Ο και της θέσης της κρούσης, των δύο σφαιρών.

ii) Να αποδείξετε ότι η κρούση μεταξύ της σφαίρας Β και του εδάφους, είναι ανελαστική.

iii) Να υπολογίσετε την μεταβολή της ορμής της Β σφαίρας κατά την κρούση των δύο σφαιρών.

iv) Να υπολογιστεί η απώλεια της μηχανικής ενέργειας κατά την κρούση της σφαίρας Β με το έδαφος.

Δίνεται g=10m/s².

Απάντηση:

ή

 Δύο κρούσεις, ένας έλεγχος

 Δύο κρούσεις, ένας έλεγχος

Η πτώση δύο πλαισίων

1) Ένας κατακόρυφος αγωγός, πολύ μεγάλου μήκους, διαρρέεται από συνεχές ρεύμα σταθερής έντασης Ι, με φορά προς τα πάνω. Δίπλα στον αγωγό, σε μικρή απόσταση, κρατάμε ένα χάλκινο πλαίσιο, έτσι ώστε ο αγωγός να βρίσκεται στο επίπεδο που ορίζει το πλαίσιο. Σε μια  στιγμή αφήνουμε το πλαίσιο να πέσει.

i)  Το πλαίσιο θα αρχίσει να διαρρέεται από ρεύμα λόγω επαγωγής.

ii)  Το πλαίσιο θα πλησιάσει τον αγωγό εξαιτίας της δύναμης Laplace που θα δεχτεί από το μαγνητικό πεδίο του αγωγού.

iii) Το πλαίσιο θα απομακρυνθεί από τον αγωγό εξαιτίας της δύναμης Laplace, που θα δεχτεί από το μαγνητικό πεδίο του αγωγού.

iv) Η κίνηση του πλαισίου θα είναι ελεύθερη πτώση.

Ποιες από τις παραπάνω προτάσεις είναι σωστές; Να δώσετε σύντομες δικαιολογήσεις.

Η αντίσταση του αέρα θεωρείται αμελητέα.

Συνέχεια:

ή

Η πτώση δύο πλαισίων

Η πτώση δύο πλαισίων