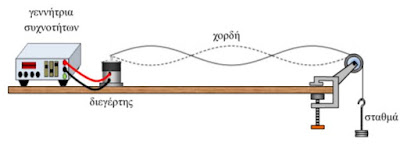
Μία ομάδα μαθητών χρησιμοποίησε την πιο κάτω
πειραματική διάταξη για τη δημιουργία στάσιμου κύματος σε χορδή. Το μήκος της
χορδής είναι 2,40 m. Ο διεγέρτης ταλαντώνεται με συχνότητα 12 Hz και στη χορδή
δημιουργείται στάσιμο κύμα με τρεις βρόχους όπως φαίνεται στο πιο πάνω σχήμα.
(α) Να εξηγήσετε πώς δημιουργείται…
Τρίτη 29 Μαΐου 2018
Κυπριακές εξετάσεις στη Φυσική 2018
2. Το παρακάτω σχήµα δείχνει ένα καροτσάκι µιας
υπεραγοράς. Το σχήµα δεν έχει σχεδιαστεί υπό κλίµακα. Το βάρος του καροτσιού
είναι 160 N.
(α) Να διατυπώσετε τις αναγκαίες συνθήκες στατικής
ισορροπίας ενός στερεού σώµατος. (Mονάδες 2)
(β) Να υπολογίσετε το µέτρο της ελάχιστης δύναµης που
πρέπει να εφαρµοστεί κατακόρυφα στο σηµείο Α για την ανύψωση των µπροστινών
τροχών του καροτσιού από το έδαφος.
2018_05_18_038_themata
Κυριακή 27 Μαΐου 2018
Στερεά κυκλικής διατομής. Δυο εφαρμογές.
Εφαρμογή 1η:
Δυο όμοιες σφαίρες συγκρατούνται πάνω σε δύο κεκλιμένα
επίπεδα, στο ίδιο ύψος h από το οριζόντιο επίπεδο. Σε μια στιγμή τις αφήνουμε
ταυτόχρονα να κινηθούν. Αν το αριστερό επίπεδο είναι λείο, ενώ η Β σφαίρα
κυλίεται:
i)
Όταν οι σφαίρες φτάσουν στο οριζόντιο επίπεδο:
α)
Μεγαλύτερη κινητική ενέργεια θα έχει η Α σφαίρα.
β)
Μεγαλύτερη κινητική ενέργεια θα έχει η Β σφαίρα.
γ)
Οι δύο σφαίρες θα έχουν ίσες κινητικές ενέργειες.
ii)
Πρώτη θα φτάσει στο οριζόντιο επίπεδο:
α)
Η Α σφαίρα, β) Η Β σφαίρα, γ) Οι δυο σφαίρες θα φτάσουν ταυτόχρονα στο
οριζόντιο επίπεδο.
Εφαρμογή 2η:
Τα δύο κεκλιμένα επίπεδα του διπλανού σχήματος,
παρουσιάζουν τον ίδιο συντελεστή τριβής με τα στερεά κυκλικής διατομής Α και Β,
τα οποία συγκρατούνται στο ίδιο ύψος h από το οριζόντιο επίπεδο. Τα δυο στερεά
έχουν ίσες μάζες και αφήνοντάς τα να κινηθούν κυλίονται και φτάνουν στο οριζόντιο
επίπεδο, με πρώτο το Β.
i) Όταν τα δυο στερεά φτάσουν στο οριζόντιο
επίπεδο:
α)
Μεγαλύτερη κινητική ενέργεια θα έχει το Α.
β)
Μεγαλύτερη κινητική ενέργεια θα έχει το Β.
γ)
Τα δυο στερεά θα έχουν ίσες κινητικές
ενέργειες.
ii)
Αν Ι1 η ροπή αδράνειας του Α στερεού ως προς τον άξονα περιστροφής
του και Ι2 και η αντίστοιχη ροπή αδράνειας του Β, ισχύει:
α)
Ι1 < Ι2, β) Ι1
= Ι2, γ) Ι1
> Ι2.
ή
Σάββατο 26 Μαΐου 2018
Στηρίζουμε μια σκάλα σε τοίχο
Ένας ελαιοχρωματιστής θέλει να
τοποθετήσει μια σκάλα, η οποία να στηρίζεται σε μη λείο κατακόρυφο τοίχο, σε δωμάτιο
με λείο δάπεδο, όπως στο σχήμα.
i) Μπορεί να το
κάνει, αρκεί να επιλέξει κατάλληλη γωνία κλίσεως θ, όπου θ<90°.
ii) Δεν μπορεί
να το κάνει, ανεξαρτήτως της κλίσεως που θα επιλέξει.
Ποια από τις δύο παραπάνω θέσεις
είναι σωστή; Να δικαιολογήσετε την απάντησή σας.
ή
Πέμπτη 24 Μαΐου 2018
Ας αυξήσουμε την ταχύτητα εκροής
Ένα μεγάλο δοχείο με νερό κλείνεται με αβαρές έμβολο και
περιέχει νερό. Σε βάθος h από την πάνω επιφάνεια του νερού υπάρχει μια μικρή
οπή από την οποία εκρέει το νερό με ταχύτητα υ1.
Αν ασκήσουμε στο έμβολο κατακόρυφη δύναμη F με μέτρο ίσο
με το οκταπλάσιο του βάρους του νερού στο τμήμα του δοχείου πάνω από το οριζόντιο
επίπεδο που περνάει από την οπή, τότε η ταχύτητα εκροής του νερού υ2
θα είναι ίση:
α)
υ2=2υ1, β) υ2=3υ1,
γ) υ2=4υ1, δ) υ2=8υ1.
Να δικαιολογήσετε την επιλογή σας.
ή
Τρίτη 22 Μαΐου 2018
Η δύναμη που ασκεί το σώμα στο ελατήριο
Ένα σώμα μάζας m αφήνεται στο πάνω άκρο ενός κατακόρυφου
ελατηρίου σταθεράς k, το οποίο έχει το φυσικό μήκος του. Το σώμα εκτελεί μια
κατακόρυφη ΑΑΤ.
i) Η ενέργεια της ταλάντωσης είναι αντιστρόφως
ανάλογη της σταθεράς του ελατηρίου k.
ii)
Η μέγιστη δυναμική ενέργεια του
ελατηρίου είναι τετραπλάσια της ενέργειας ταλάντωσης.
iii)
Η μέγιστη δύναμη που ασκεί το σώμα στο ελατήριο, είναι ίση με το βάρος του.
Να
χαρακτηρίσετε τις παραπάνω προτάσεις ως σωστές ή λανθασμένες δικαιολογώντας την
απάντησή σας.
ή
Δευτέρα 21 Μαΐου 2018
Μια ακόμη ισορροπία και όχι ανατροπή
Διαθέτουμε δύο ομογενείς ράβδους ΑΟ και ΟΓ με το ίδιο
μήκος l=2m και βάρη w1=50Ν και w2=100Ν αντίστοιχα. Καρφώνουμε
τις δυο ράβδους συνδέοντας τις στο κοινό άκρο τους Ο, δημιουργώντας έτσι το
επίπεδο στερεό ΑΟΓ, (στερεό s), όπου η γωνία ΑΟΓ=120°. Τοποθετούμε το στερεό s
πάνω σε τραπέζι έτσι ώστε το επίπεδό του να είναι κατακόρυφο, όπως στο σχήμα.
i) Να υπολογιστεί το μέτρο της δύναμης που ασκεί
το τραπέζι στο στερεό s, καθώς και η ροπή της ως προς το μέσον Μ της ΟΓ.
ii)
Ποιο είναι το μέγιστο βάρος ενός σώματος Σ, το οποίο μπορούμε να κρεμάσουμε
μέσω νήματος στο μέσον Ρ της ράβδου ΑΟ, χωρίς το στερεό να ανατρέπεται;
ή
Κυριακή 20 Μαΐου 2018
Κύλιση με πλάγια δύναμη
Γύρω από έναν ομογενή κύλινδρο Α, ο οποίος ηρεμεί σε
οριζόντιο επίπεδο, έχουμε τυλίξει ένα αβαρές
και μη εκτατό νήμα. Τραβώντας το ελεύθερο άκρο του νήματος, ασκούμε στον κύλινδρο
μια σταθερού μέτρου δύναμη F, η οποία σχηματίζει με την οριζόντια διεύθυνση σταθερή
γωνία θ, οπότε ο κύλινδρος αρχίζει να κυλίεται.
i) Να
αποδειχθεί ότι το επίπεδο δεν μπορεί να είναι λείο και ότι θα ασκηθεί στον κύλινδρο
στατική τριβή με φορά προς τα δεξιά.
ii)
Ένας δεύτερος όμοιος κύλινδρος Β, ο οποίος
αρχικά ηρεμεί στο ίδιο οριζόντιο επίπεδο, δέχεται την ίδια δύναμη F στο κέντρο
μάζας του Ο, οπότε και αυτός κυλίεται. Αν ο Α κύλινδρος χρειάζεται χρόνο t1
για να μετακινηθεί κατά d, τότε ο Β για την ίδια απόσταση d, θα χρειαστεί χρόνο t2, όπου:
α) t1 < t2, α) t1 = t2, α) t1 > t2.
iii)
Μεγαλύτερη κινητική ενέργεια, μετά το τέλος της παραπάνω μετακίνησης κατά d, θα
έχει:
α) Ο κύλινδρος Α,
β) ο κύλινδρος Β, γ) θα έχουν ίσες
κινητικές ενέργειες.
Να δικαιολογήσετε αναλυτικά τις απαντήσεις σας.
Δίνεται η ροπή αδράνειας ενός κυλίνδρου Ιcm= ½
mR2, ως προς τον άξονά του ο οποίος συνδέει τα κέντρα των δύο βάσεών
του.
ή
Παρασκευή 18 Μαΐου 2018
Ένα στάσιμο κύμα και η εξίσωσή του
Πάνω σε μια χορδή, με
σταθερά τα δυο της άκρα, έχει σχηματισθεί ένα στάσιμο κύμα με πλάτος 0,2m. Παίρνοντας
το αριστερό άκρο της χορδής ως αρχή ενός άξονα x, η εξίσωση του στάσιμου μπορεί
να πάρει μια ή περισσότερες από τις παρακάτω μορφές (μονάδες στο S.Ι.):
i) y=0,2∙συν(4πx)∙ημ(πt)
ii) y=0,2∙συν(πt)∙ημ(4πx)
iii) y=0,2∙συν(πt+φ0)∙ημ(4πx)
iv) y= 0,2∙συν(4πx)∙ημ(πt+φ0)
v) y=0,2∙συν(4πt)∙ημ(πt)
vi) y= 0,2∙ημ(4πx)∙ημ(πx)
Ποιες εξισώσεις μπορούν να περιγράψουν το στάσιμο κύμα
στη χορδή;
Να δικαιολογήσετε την απόρριψη των λανθασμένων εξισώσεων
(να μην δικαιολογηθούν οι σωστές…)
ή
Πέμπτη 17 Μαΐου 2018
Το πλάτος ταλάντωσης μετά από κρούση
Μια πλάκα μάζας Μ εκτελεί
ΑΑΤ, με περίοδο Τ1 και πλάτος Α1, δεμένη στο πάνω άκρο
ενός κατακόρυφου ιδανικού ελατηρίου. Μια σφαίρα μάζας m αφήνεται να πέσει από
κάποιο ύψος και συγκρούεται (μη πλαστικά) με την πλάκα. Ελάχιστα πριν την
κρούση τα δυο σώματα έχουν ταχύτητες με φορά προς τα κάτω, όπως στο σχήμα.
Αμέσως μετά την κρούση, η σφαίρα απομακρύνεται, ενώ η πλάκα αρχίζει μια νέα
ταλάντωση.
i) Για την περίοδο Τ2 της νέας
ταλάντωσης της πλάκας, ισχύει:
α)
Τ2 < Τ1, β) Τ2
= Τ1, γ) Τ2
> Τ1.
ii) Για το νέο πλάτος
ταλάντωσης Α2 θα ισχύει:
α)
Α2<Α1, β) Α2
= Α1, α) Α2
> Α1.
Να δικαιολογήσετε τις
απαντήσεις σας.
ή
Τετάρτη 16 Μαΐου 2018
Από δεξαμενή σε δεξαμενή
Στο διπλανό σχήμα βλέπετε μια μεγάλη δεξαμενή Α που
περιέχει νερό σε βάθος h, από την βάση της οποίας ξεκινά ένας σωλήνας διατομής
Α1, μέσω του οποίου τροφοδοτείται μια δεύτερη δεξαμενή Β. Από τη βάση
της Β δεξαμενής ξεκινά ένας δεύτερος σωλήνας
διπλάσιας διατομής (Α2=2Α1), ο οποίος μεταφέρει νερό σε μια
τρίτη δεξαμενή Γ. Στο σχήμα έχουν σημειωθεί οι κατακόρυφες αποστάσεις, μεταξύ
των διαφόρων επιφανειών. Αν το ύψος y
του νερού στη δεξαμενή Β δεν μεταβάλλεται με το χρόνο, τότε το ύψος y είναι
ίσο:
α)
y=0,5h, β) y=0,75h,
γ) y=1h, δ) y=1,25h.
Η δεξαμενή Α θεωρείται πολύ μεγάλη και η στάθμη του
νερού στο εσωτερικό της παραμένει πρακτικά σταθερή.
ή
Κυριακή 13 Μαΐου 2018
Η ανατροπή και η κύλιση
Ερώτηση 1η :
Σε τραχύ οριζόντιο επίπεδο ηρεμεί ένα ομογενές ορθογώνιο
παραλληλεπίπεδο, με πλευρές α και 2α, βάρους w. Σε μια στιγμή ασκούνται πάνω του δύο οριζόντιες δυνάμεις
μέτρου F= 1/4w, όπως στο σχήμα.
i) Αναφερόμενοι
στην τριβή που θα ασκηθεί στο στερεό:
α) Θα
ασκηθεί πάνω του δύναμη τριβής με φορά προς τα δεξιά.
β) Θα
ασκηθεί πάνω του δύναμη τριβής με φορά προς τα αριστερά.
γ)
Δεν θα εμφανισθεί δύναμη τριβής.
ii)
Αναφερόμενοι στο ενδεχόμενο ανατροπής του ορθογωνίου:
α) Πρόκειται
να ανατραπεί γύρω από την κορυφή Γ.
β) Πρόκειται
να ανατραπεί γύρω από την κορυφή Δ.
γ)
Δεν πρόκειται να ανατραπεί.
Ερώτηση 2η:
Σε τραχύ οριζόντιο επίπεδο ηρεμεί ένας ομογενής κύλινδρος
μάζας m και ακτίνας R. Σε μια στιγμή ασκούνται πάνω του δύο οριζόντιες δυνάμεις
μέτρου F, όπως στο σχήμα (η μια στο κέντρο μάζας Ο και η δεύτερη μέσω νήματος
που έχουμε τυλίξει γύρω του, στο ανώτερο σημείο Α).
i) Αναφερόμενοι
στην τριβή που θα ασκηθεί στον κύλινδρο:
α) Θα
ασκηθεί πάνω του δύναμη τριβής με φορά προς τα δεξιά.
β) Θα
ασκηθεί πάνω του δύναμη τριβής με φορά προς τα αριστερά.
γ)
Δεν θα εμφανισθεί δύναμη τριβής.
ii)
Αν ο κύλινδρος κυλίεται (χωρίς να ολισθαίνει), τότε το μέτρο της ασκούμενης
τριβής είναι:
α)
Τ=0, β) Τ= 1/3 F, γ) Τ= 2/3 F, δ) Τ=F.
Δίνεται η ροπή αδράνειας του κυλίνδρου ως προς τον άξονα
περιστροφής του Ι= ½ mR2.
ή
Σάββατο 12 Μαΐου 2018
Ένας κύλινδρος σε λείο κεκλιμένο επίπεδο
Γύρω από έναν ομογενή κύλινδρο μάζας m, τυλίγουμε ένα
αβαρές και μη εκτατό νήμα. Τοποθετούμε τον κύλινδρο σε λείο κεκλιμένο επίπεδο
κλίσεως θ και ασκούμε στο άκρο Α του νήματος, σταθερή δύναμη F, παράλληλη με το
επίπεδο και μέτρου F= ½ mg∙ημθ.
i)
Ο κύλινδρος θα κινηθεί κατά μήκος του επιπέδου:
α) προς τα πάνω,
β) προς τα κάτω, γ) δεν θα
κινηθεί κατά μήκος του επιπέδου.
ii)
Μέσω του έργου της δύναμης F:
α)
μεταφέρεται ενέργεια στον κύλινδρο,
β)
αφαιρείται ενέργεια από τον κύλινδρο,
γ)
τίποτα από τα δύο.
iii)
Μετά από κάποιο χρονικό διάστημα, η κινητική ενέργεια του κυλίνδρου εμφανίζεται
σαν μεταφορική κινητική ενέργεια Κμ και σαν στροφική κινητική
ενέργεια Κπ. Ο λόγος Κμ/Κπ είναι ίσος με:
α) ½ , β)
1, γ) 2.
Να δικαιολογήσετε αναλυτικά τις απαντήσεις σας.
Δίνεται η ροπή αδράνειας του κυλίνδρου ως προς τον άξονά
του Ι= ½ mR2.
ή
Πέμπτη 10 Μαΐου 2018
Ισορροπία και κίνηση ενός συστήματος
Το σώμα Σ1 μάζας m1=4kg
ηρεμεί σε λείο οριζόντιο επίπεδο, δεμένο στο άκρο ιδανικού ελατηρίου σταθεράς
k=250Ν/m. Δένουμε το σώμα με αβαρές και μη εκτατό νήμα, το οποίο αφού περάσουμε
από μια τροχαλία, στο άλλο άκρο του δένουμε ένα δεύτερο σώμα Σ2
μάζας m2=1kg. Ασκώντας μια κατακόρυφη δύναμη F=90Ν συγκρατούμε ακίνητο
το Σ2 όπως στο σχήμα.
Δίνεται ότι η τροχαλία μπορεί να
στρέφεται χωρίς τριβές γύρω από τον άξονά της, έχοντας ροπή αδράνειας Ι= ½ ΜR2,
το νήμα δεν γλιστρά στο αυλάκι της τροχαλίας, ενώ g=10m/s2.
i) Να
υπολογιστεί η δυναμική ενέργεια του ελατηρίου κατά την ισορροπία του συστήματος.
ii)
Σε μια στιγμή t0=0, παύουμε να ασκούμε την δύναμη F. Αν η αρχική
επιτάχυνση του σώματος Σ2 είναι α02=11,25m/s2,
να βρεθεί η μάζα της τροχαλίας.
iii)
Μετά από λίγο, τη στιγμή t1, μηδενίζεται στιγμιαία η επιτάχυνση του
σώματος Σ2.
α)
Να βρεθεί η συνολική κινητική ενέργεια του συστήματος των τριών σωμάτων τη στιγμή
t1.
β)
Ποιος ο ρυθμός μεταβολής της στροφορμής της τροχαλίας, ως προς τον άξονά της τη
στιγμή t1;
iv)
Αν τη στιγμή t2 που η ταχύτητα του σώματος Σ2 γίνει ίση
με 2m/s, για δεύτερη φορά, κόψουμε το νήμα που συνδέει τα σώματα, να βρεθούν:
α) Η ενέργεια της ταλάντωσης του σώματος Σ1.
β) Ποιο από τα παρακάτω ποιοτικά διαγράμματα,
μπορεί να παριστά τη στροφορμή της τροχαλίας ως προς τον άξονα περιστροφής της,
σε συνάρτηση με το χρόνο;
Να δικαιολογήσετε την
επιλογή σας.
ή
Τρίτη 8 Μαΐου 2018
Η ενέργεια κυλίνδρου με πλάγια δύναμη
Ένας ομογενής κύλινδρος ηρεμεί σε λείο οριζόντιο επίπεδο,
ενώ γύρω του έχουμε τυλίξει, ένα μακρύ αβαρές
νήμα. Τραβάμε το άκρο Α του νήματος, όπως στο σχήμα, ασκώντας του δύναμη F. Μετά
από λίγο ο κύλινδρος έχει ταχύτητα κέντρου μάζας υcm.
 Η ενέργεια κυλίνδρου με πλάγια δύναμη
Η ενέργεια κυλίνδρου με πλάγια δύναμη
Το έργο της δύναμης στο παραπάνω χρονικό διάστημα είναι:
α) WF
< 1,5∙ ½ mυcm2 β) WF = 1,5∙½mυcm2, γ) WF > 1,5∙½mυcm2.
Να δικαιολογήσετε την απάντησή σας.
Δίνεται η ροπή αδράνειας του κυλίνδρου ως προς τον άξονα
περιστροφής του Ι= ½ mR2.
ή
 Η ενέργεια κυλίνδρου με πλάγια δύναμη
Η ενέργεια κυλίνδρου με πλάγια δύναμηΠαρασκευή 4 Μαΐου 2018
Γιατί το «να κόβεις δρόμο» είναι καλό και για επιταχύνσεις…
Η ανάρτηση απευθύνεται μόνο σε καθηγητές και είναι
συνέχεια μιας παλιότερης:
Περιέχει λίγη θεωρία και μια εφαρμογή:
Εφαρμογή:
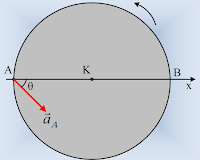
Ένας ομογενής οριζόντιος δίσκος ακτίνας R=1m, κινείται σε λείο οριζόντιο επίπεδο με την επίδραση
κατάλληλης δύναμης F. Κάποια στιγμή που ο δίσκος έχει γωνιακή ταχύτητα ω=1rad/s και
γωνιακή επιτάχυνση αγων=3rad/s2, διανύσματα κατακόρυφης
διεύθυνσης με φορά προς τα πάνω, το σημείο Α στο άκρο μιας ακτίνας στη
διεύθυνση x, έχει επιτάχυνση μέτρου αΑ=5m/s2 η οποία
σχηματίζει γωνία θ (ημθ=0,6) με την ακτίνα, όπως στο σχήμα.
Να υπολογιστούν:
1) Η επιτάχυνση του κέντρου μάζας Κ του δίσκου
2) Η επιτάχυνση του αντιδιαμετρικού σημείου Β του δίσκου.
Διαβάστε τη συνέχεια…
ή
Πέμπτη 3 Μαΐου 2018
Η ισορροπία και η κίνηση της στεφάνης
Γύρω από μια στεφάνη μάζας 2kg έχουμε τυλίξει ένα αβαρές
και μη εκτατό νήμα. Τοποθετούμε τη στεφάνη σε κεκλιμένο επίπεδο κλίσεως θ=30°
και ασκώντας στο άκρο Α του νήματος δύναμη F, παράλληλη στο επίπεδο, η στεφάνη
ισορροπεί.
i)
Να αποδείξετε ότι το επίπεδο δεν είναι λείο και να υπολογίσετε το μέτρο της
ασκούμενης δύναμης F.
ii)
Κάποια στιγμή t0=0, μεταβάλλουμε το μέτρο της δύναμης στην τιμή F1=4Ν,
οπότε έχουμε την κίνηση της στεφάνης. Αν οι συντελεστές τριβής μεταξύ στεφάνης
και επιπέδου είναι μ=μs=√3/2, να αποδείξτε ότι η ασκούμενη τριβή
είναι στατική, υπολογίζοντας το μέτρο
της.
iii)
Να υπολογιστούν τη χρονική στιγμή t1=4s:
α) η ταχύτητα του κέντρου μάζας Ο της στεφάνης,
καθώς και η κινητικής της ενέργεια.
β) Η ισχύς κάθε δύναμης που ασκείται στη
στεφάνη.
γ)
Ο ρυθμός μεταβολής της κινητικής ενέργειας της στεφάνης.
iv)
Να υπολογιστούν τα έργα των δυνάμεων που ασκούνται στη στεφάνη από 0-t1.
Δίνονται ότι: Η μάζα της στεφάνης θεωρείται συγκεντρωμένη
στην περιφέρειά της, ενώ g=10m/s2 και ημ30°= ½, συνθ=√3/2.
Τετάρτη 2 Μαΐου 2018
Ο δακτύλιος και η ράβδος σαν στερεό
Έχουμε κατασκευάσει ένα στερεό s με συγκόλληση ενός
δακτυλίου μάζας m και ακτίνας R και μιας ομογενούς ράβδου ΑΒ μήκους l=2R και
μάζας Μ=3m, όπως στο διπλανό σχήμα. Το στερεό s, μπορεί να στρέφεται σε
κατακόρυφο επίπεδο, γύρω από οριζόντιο άξονα που περνά από το σημείο Ο,
αντιδιαμετρικό του σημείου Α που έχει συγκολληθεί η ράβδος. Το στερεό συγκρατείται
σε τέτοια θέση που η ράβδος να είναι οριζόντια.
i)
Η ροπή αδράνειας του στερεού s ως προς τον άξονα περιστροφής στο Ο έχει τιμή:
α) ΙΑ= 20mR2,
β) ΙΑ= 25mR2,
γ) ΙΑ= 30mR2,
δ) ΙΑ= 35mR2.
ii)
Αφήνουμε το στερεό να κινηθεί σε κατακόρυφο επίπεδο. Η αρχική επιτάχυνση του
άκρου Β της ράβδου έχει μέτρο:
α) αΒ
< g, β) αΒ = g, γ) αΒ > g.
iii)
Η μέγιστη κινητική ενέργεια που θα αποκτήσει κατά την παραπάνω κίνηση ο
δακτύλιος είναι:
α) Κmax < mgR, β) Κmax = mgR, γ) Κmax
> mgR.
Δίνεται ότι ο μάζα του δακτυλίου θεωρείται συγκεντρωμένη
στην περιφέρειά του, ενώ η ροπή αδράνειας μιας ομογενούς ράβδου ως προς κάθετο
άξονα που περνά από το ένα της άκρο ΙΒ= ml2/3.
ή
Εγγραφή σε:
Αναρτήσεις (Atom)