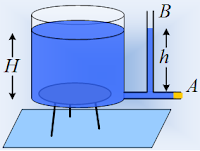
Ένα μεγάλο κυλινδρικό δοχείο περιέχει νερό σε βάθος Η,
ενώ κοντά στον πυθμένα του είναι συνδεδεμένος οριζόντιος σωλήνας Α. Στον σωλήνα
αυτό έχει συνδεθεί δεύτερος κατακόρυφος σωλήνας Β.
Παρακάτω δίνονται τρεις εκδοχές, θεωρώντας το νερό
ιδανικό ρευστό:
Εκδοχή 1η :
Ο σωλήνας Α φράσσεται με τάπα, ενώ ο Β είναι ανοικτός.
i) Για το ύψος του νερού στο σωλήνα Β ισχύει:
α)
h<Η, β) h=Η, γ) h>Η
ii) Ανοίγουμε την τάπα και αποκαθίσταται μόνιμη και
στρωτή ροή. Για το νέο ύψος του νερού στο σωλήνα Β ισχύει:
α)
h=Η, β) h<Η, γ) h=0
Εκδοχή 2η :
Ο σωλήνας Α φράσσεται με τάπα, ενώ ο Β είναι κλειστός
και γεμάτος με νερό μέχρι ύψος h=2m, ενώ h>Η.
i) Για την τιμή της πίεσης στο κάτω μέρος του σωλήνα Β,
σημείο Κ ισχύει:
α)
pΚ=ρgh , β) pΚ=ρgΗ, γ) pΚ=pατμ+ ρgh, δ) pΚ=pατμ+ ρgΗ
ii) Ανοίγουμε την τάπα και αποκαθίσταται μόνιμη και
στρωτή ροή. Για το νέο ύψος του νερού στο σωλήνα Β ισχύει:
α)
h1 =h, β) h1
=Η, γ) h1 < Η, δ) h1=0.
Εκδοχή 3η :
Ο σωλήνας Α φράσσεται με τάπα, ενώ ο Β είναι κλειστός
έχοντας εγκλωβισμένη κάποια ποσότητα αέρα ενώ το νερό έχει ανέλθη κατά h=Η.
i) Για την τιμή της πίεσης στο κάτω μέρος του σωλήνα Β,
σημείο Κ ισχύει:
α)
pΚ=ρgh , β) pΚ=pατμ+
ρgh, γ) pΚ > pατμ+
ρgΗ
ii) Ανοίγουμε την τάπα και αποκαθίσταται μόνιμη και
στρωτή ροή. Για το νέο ύψος του νερού στο σωλήνα Β ισχύει:
α)
h1 =h, β) h1 <
Η, γ) h1=0.
Δίνονται pατμ=105Ν/m2,
η πυκνότητα του νερού ρ=1.000kg/m3 και g=10m/s2.
ή
| Τρεις εκδοχές σε παρόμοια φαινόμενα. |



Δεν υπάρχουν σχόλια:
Δημοσίευση σχολίου