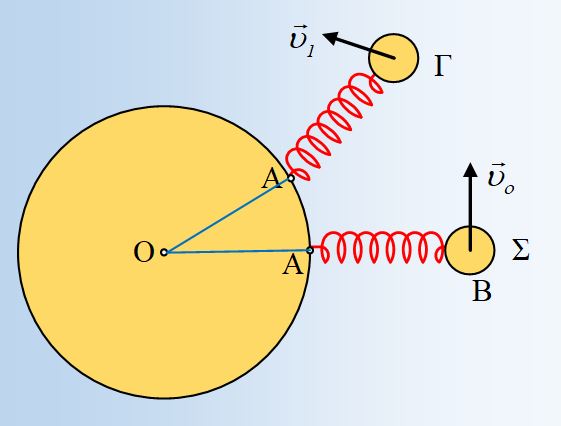
Σε λείο οριζόντιο επίπεδο ηρεμεί ένας ομογενής δίσκος μάζας Μ=8kg και ακτίνας R=1m, ο οποίος μπορεί να στρέφεται χωρίς τριβές, γύρω από κατακόρυφο άξονα ο οποίος περνά από το κέντρο του Ο. Σε ένα σημείο Α, στο άκρο μιας ακτίνας του δίσκου δένουμε ένα ιδανικό ελατήριο, στο άλλο άκρο του οποίου έχουμε δέσει ένα σώμα Σ, μάζας m= 2kg, το οποίο θεωρούμε υλικό σημείο, το οποίο επίσης ηρεμεί, στη θέση Β. Το ελατήριο έχει σταθερά k=200Ν/m και φυσικό μήκος lο=1m και ο άξονάς του βρίσκεται στην προέκταση της ακτίνας (ΟΑ). Σε μια στιγμή t0=0, δίνουμε ένα κτύπημα στο σώμα Σ, με αποτέλεσμα να αποκτήσει οριζόντια αρχική ταχύτητα μέτρου υ0=4m/s, κάθετη στην απόσταση (ΟΒ), όπως στο σχήμα (σε κάτοψη).
i) Να υπολογιστεί η αρχική στροφορμή του σώματος Σ ως προς τον άξονα περιστροφής του δίσκου στο Ο.
ii) Μετά από λίγο, τη στιγμή t1 το σώμα Σ φτάνει στη θέση Γ, όπου ξανά το ελατήριο έχει το φυσικό μήκος του. Τη στιγμή αυτή ο δίσκος στρέφεται αντίθετα από τους δείκτες του ρολογιού με γωνιακή ταχύτητα ω1=1,5rad/s.
α) Να υπολογιστεί ξανά η στροφορμή του σώματος Σ ως προς τον άξονα στο κέντρο Ο, τη στιγμή αυτή.
β) Να βρεθεί η απόσταση d του Ο από τον φορέα της ταχύτητας υ1 του σώματος Σ
γ) Να υπολογιστεί το έργο της δύναμης του ελατηρίου που ασκήθηκε στο δίσκο από t0 έως τη στιγμή t1.
iii) Σε μια επόμενη στιγμή t2 το σώμα Σ φτάνει σε μια νέα θέση Δ, με ταχύτητα μέτρου υ2=1,5m/s, ενώ το μήκος του ελατηρίου είναι 1,1m. Για την στιγμή αυτή να υπολογιστούν:
α) Η γωνιακή ταχύτητα περιστροφής του δίσκου, δεδομένου ότι έχει την ίδια κατεύθυνση με πριν.
β) Η στροφορμή του σώματος Σ ως προς τον άξονα περιστροφής στο Ο.
Δίνεται ότι ένα υλικό σημείο το οποίο κινείται με ταχύτητα υ, παρουσιάζει ως προς ένα τυχαίο σημείο Κ, στροφορμή μέτρου L=mυ∙d, όπου d η απόσταση του σημείου Κ από τον φορέα της δύναμης, με κατεύθυνση όπως στο σχήμα
ή


Δεν υπάρχουν σχόλια:
Δημοσίευση σχολίου