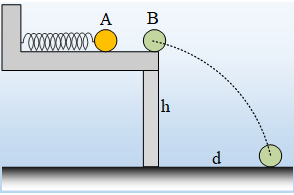
Σε ένα οριζόντιο λείο υπερυψωμένο σκαλοπάτι ηρεμούν δύο σφαίρες Α και Β, της ίδιας ακτίνας, σε ύψος h=0,8m από το έδαφος, η πρώτη δεμένη στο άκρο ιδανικού ελατηρίου, όπως στο σχήμα. Απομακρύνουμε την σφαίρα Α, από την θέση ισορροπίας της, συμπιέζοντας το ελατήριο και τη στιγμή t0=0 την αφήνουμε να κινηθεί και να εκτελέσει αατ, με εξίσωση απομάκρυνσης:
x=0,5∙ημ(10t+ 3π/2).
Την χρονική στιγμή t1=π/12s η σφαίρα Α συγκρούεται κεντρικά και ελαστικά με την σφαίρα Β, η οποία πέφτει στο έδαφος σε οριζόντια απόσταση d=h.
i) Να βρεθεί η αρχική απόσταση των δύο σφαιρών, καθώς και η ταχύτητα της Α σφαίρας ελάχιστα πριν την κρούση.
ii) Να βρεθεί η ταχύτητα της Β σφαίρας, τη στιγμή που φτάνει στο έδαφος;
iii) Να υπολογιστεί η σταθερά του ελατηρίου, αν δίνεται η μάζα της Β σφαίρας m2=1,5kg.
iv) Αν Ε1 η ενέργεια της ταλάντωσης της Α σφαίρας πριν την κρούση και Ε2 μετά από την κρούση, να βρεθεί ο λόγος Ε2/Ε1.
Δίνεται g=10m/s2.
ή

Δεν υπάρχουν σχόλια:
Δημοσίευση σχολίου