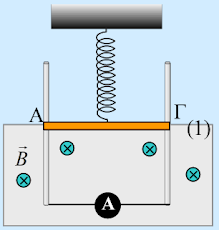
Μια ομογενής λεπτή αγώγιμη ράβδος μάζας 2kg, ισορροπεί στο κάτω άκρο ενός κατακόρυφου ιδανικού ελατηρίου, στην θέση (1), μέσα σε ένα ομογενές οριζόντιο μαγνητικό πεδίο, με δυναμικές γραμμές κάθετες στο επίπεδο της σελίδας, όπως στο σχήμα, σε επαφή με δύο αγώγιμους κατακόρυφους στύλους. Το μαγνητικό πεδίο εκτείνεται στο χώρο, από την θέση (1) και χαμηλότερα. Οι στύλοι είναι λείοι, δεν παρουσιάζουν αντίσταση, ενώ τα κάτω τους άκρα συνδέονται μέσω ενός αμπερομέτρου. Ανεβάζουμε την ράβδο κατακόρυφα κατά h και την αφήνουμε να κινηθεί, οπότε φτάνοντας στην θέση (1), εισέρχεται στο μαγνητικό πεδίο, οπότε αμέσως μετά την είσοδο, τη στιγμή t1, έχει ταχύτητα μέτρου υ=2m/s και επιτάχυνση μέτρου α=0,5m/s2.
i) Για τη στιγμή t1, αμέσως μετά την είσοδο, να βρεθούν οι ρυθμοί μεταβολής:
α) της βαρυτικής δυναμικής ενέργειας.
β) της δυναμικής ενέργειας του ελατηρίου.
γ) της κινητικής ενέργειας της ράβδου.
Ποια η ηλεκτρική ισχύς που εμφανίζεται στο κύκλωμα, τη στιγμή t1;
ii) Αν τη στιγμή t1 το αμπερόμετρο δείχνει ένδειξη 1Α, να βρεθεί η εσωτερική αντίσταση του αμπερομέτρου, αν η ράβδος έχει αντίσταση R=1,5Ω.
iii) Αν h=0,4m και y η απόσταση που θα διανύσει μέσα στο πεδίο η ράβδος, μέχρι να σταματήσει η προς τα κάτω κίνησή της, τότε:
α) y < h, β) y = h, γ) y > h.
Να δικαιολογήσετε την επιλογή σας.
iv) Να εξηγήσετε γιατί μετά από λίγο χρόνο η ράβδος ακινητοποιείται. Πόση συνολικά θερμότητα εκλύεται στις αντιστάσεις του κυκλώματος, κατά τη διάρκεια της κίνησης της ράβδου;
Δίνεται g=10m/s2.
ή

Δεν υπάρχουν σχόλια:
Δημοσίευση σχολίου