Γωνιακή επιτάχυνση ράβδου και επιτάχυνση σώματος δεμένο με νήμα με αυτήν.

Μια ομογενής οριζόντια δοκός ΑΓ μάζας m=10kg και μήκους 6m είναι αρθρωμένη στο άκρο της Α, ενώ στο άκρο της Γ είναι δεμένη με κατακόρυφο νήμα. Στο σημείο Δ της δοκού, όπου (ΑΔ)=2m, έχουμε κρεμάσει με νήμα μια σφαίρα Σ μάζας m₁=6kg, όπως στο σχήμα. Σε μια στιγμή κόβεται το νήμα στο άκρο Γ. Για αμέσως μετά το κόψιμο του νήματος να βρεθούν:

i) Η γωνιακή επιτάχυνση της δοκού και

ii) Η επιτάχυνση της σφαίρας Σ.

iii) Αν (ΑΔ)=5m ποιες οι αντίστοιχες απαντήσεις σας;

Δίνεται η ροπή αδράνειας μιας δοκού ως προς κάθετο άξονα ο οποίος διέρχεται από το άκρον της Ι= 1/3 m·l² και g=10m/s².

Απάντηση

Γωνιακή επιτάχυνση ράβδου και επιτάχυνση σώματος..

Δύναμη από τον άξονα περιστροφής.

Συνισταμένη δύναμη και cm.

Ένα στερεό στρέφεται γύρω από έναν σταθερό άξονα. Τι συμβαίνει με την συνισταμένη των δυνάμεων που ασκούνται πάνω του;

α) Αν ο άξονας περνά από το κέντρο μάζας του στερεού, τότε το κέντρο μάζας παραμένει ακίνητο, οπότε ΣF=0.

β) Αν ο άξονας δεν περνά από το κέντρο μάζας, τότε θα εφαρμόσουμε τον θεμελιώδη της Μηχανικής για το κέντρο μάζας.

Πρέπει να τονισθεί ότι όταν το στερεό στρέφεται, το κέντρο μάζας του, εκτελεί κυκλική κίνηση με κέντρο το σημείο Α του άξονα.

Οπότε εφαρμόζουμε δυναμική για ένα υλικό σημείο που εκτελεί κυκλική κίνηση.

Έτσι αν η γωνιακή ταχύτητα του στερεού σώματος, παραμένει σταθερή το κέντρο μάζας θα εκτελεί ομαλή κυκλική κίνηση, οπότε η συνισταμένη θα είναι ίση με την κεντρομόλο:

ΣF_R=mα_κ

ενώ αν υπάρχει γωνιακή επιτάχυνση του στερεού, το κέντρο μάζας θα έχει επιτρόχια επιτάχυνση και η συνισταμένη των δυνάμεων στη διεύθυνση της εφαπτομένης της κυκλικής τροχιάς θα είναι:

ΣF_εφ= mα_cm.

Παράδειγμα.

Μια ράβδος στρέφεται γύρω από οριζόντιο άξονα που περνά από το ένα του άκρο Α και έστω ότι βρίσκεται στη θέση του διπλανού σχήματος, ενώ πάνω της ασκείται το βάρος της w, μια δύναμη F στο άκρο της Β και μια δύναμη από τον άξονα, η οποία αναλύεται στις συνιστώσες F_1x και F_1y.

Ας αναλύσουμε το βάρος σε μια διεύθυνση παράλληλη προς τη ράβδο w_x και μια w_y κάθετη στην ράβδο.

Εφαρμόζουμε τον θεμελιώδη νόμο της Μηχανικής, θεωρώντας ότι όλη η μάζα της ράβδου είναι συγκεντρωμένη στο κέντρο μάζας Ο και ότι όλες οι δυνάμεις ασκούνται στο Ο και παίρνουμε:

 ΣF_καθ =mα_cm ή W_y –F_1y = mα_cm

Δηλαδή στην διεύθυνση της ακτίνας η συνισταμένη των δυνάμεων πάιζει το ρόλο της κεντρομόλου, ενώ σε κάθετη διεύθυνση η συνισταμένη είναι υπεύθυνη για την επιτάχυνση του κέντρου μάζας.

Τεστ Ισορροπίας στερεού

Η ομογενής ράβδος ΑΒ έχει μήκος 6m, μάζα Μ=15kg και ισορροπεί όπως στο σχήμα στηριζόμενη στο τρίποδο στο σημείο Γ, όπου (ΑΓ) =2m και σε κύλινδρο στο σημείο Δ με (ΔΒ)=1m.

1. Bρείτε τις δυνάμεις που ασκούνται στη ράβδο στα σημεία στήριξης.
2. Σε μια στιγμή θέτουμε σε περιστροφή τον κύλινδρο με φορά όπως οι δείκτες του ρολογιού. Αν ο συντελεστής τριβής ολίσθησης κυλίνδρου-ράβδου είναι μ=0,6 και η ράβδος συνεχίζει να ισορροπεί, να βρείτε την τριβή που ασκείται στη ράβδο από τον κύλινδρο.
3. Ποιος ο ελάχιστος συντελεστής της οριακής στατικής τριβής μεταξύ ράβδου και τρίποδου για να εξασφαλίζεται η ισορροπία της ράβδου;
4. Ποια η μέγιστη κατακόρυφη δύναμη με φορά προς τα κάτω που πρέπει να ασκηθεί στο άκρο Α, χωρίς να ανατρέπεται η ράβδος; Πόση θα είναι τότε η τριβή που δέχεται η ράβδος από το τρίποδο;

Δίνεται g=10m/s².

.

Απάντηση:

Μπορείτε να δείτε όλο το Τεστ από ΕΔΩ

Ροπή αδράνειας και γωνιακή επιτάχυνση

Οι ομογενείς ράβδοι ΟΑ και ΑΒ με ίσες μάζες m=3kg και μήκη l₁=4m και l₂=6m αντίστοιχα, είναι συγκολλημένες όπως στο σχήμα. Το σύστημα μπορεί να στρέφεται γύρω από οριζόντιο άξονα, ο οποίος περνά από το άκρο Ο. Φέρνουμε το σύστημα σε τέτοια θέση, ώστε η ράβδος ΟΑ να είναι οριζόντια και το αφήνουμε να κινηθεί.Αν η ροπή αδράνειας μιας ράβδους ως προς κάθετο άξονα που περνά από το μέσον της δίνεται από τη σχέση Ι=1/12 ml², να βρεθούν:

α) Η αρχική γωνιακή επιτάχυνση του συστήματος.

β) Η αρχική επιτάχυνση του μέσου O της ράβδου ΑΒ και να σχεδιαστεί στο σχήμα.

Απάντηση:

Κύλιση ή ολίσθηση του κυλίνδρου;

Ένας κύλινδρος βρίσκεται σε οριζόντιο επίπεδο και δέχεται την επίδραση σταθερής οριζόντιας δύναμης F η οποία ασκείται σε σημείο Α της περιφέρειάς του, όπως στο σχήμα.

i) Η ροπή της δύναμης:

α) έχει φορά προς τα δεξιά.

β) Είναι οριζόντια με μέτρο τ=FR.

γ) Είναι κάθετη στο επίπεδο της σελίδας με φορά προς τα μέσα στο σημείο Α.

δ) Είναι κάθετη στο επίπεδο της σελίδας με φορά προς τα μέσα στο σημείο Ο και μέτρο μικρότερο από το γινόμενο FR.

ii) Χαρακτηρίστε σαν σωστές ή λαθεμένες τις παρακάτω προτάσεις.

α) Ο κύλινδρος θα αποκτήσει γωνιακή επιτάχυνση προς τα δεξιά.

β) Η γωνιακή επιτάχυνση του κυλίνδρου έχει σταθερό μέτρο.

γ) Η γωνιακή ταχύτητα του κυλίνδρου θα δίνεται από τη σχέση ω=α_γωνt.

δ) Η επιτάχυνση του σημείου Α έχει την κατεύθυνση της δύναμης F.

iii) Αν το επίπεδο είναι λείο:

α) Ο αρχικός ρυθμός μεταβολής της στροφορμής του κυλίνδρου είναι ίσος με μηδέν.

β) Η αρχική ισχύς της δύναμης είναι μηδενική.

γ) Ο κύλινδρος θα κυλίεται χωρίς να ολισθαίνει.

δ) Η αρχική επιτάχυνση του σημείου Γ είναι μηδενική.

Απάντηση

Πότε έχουμε καλύτερη ισορροπία;

Δίνεται μια αβαρής ράβδος ΑΒ μήκους 1m, σε σημείο Γ της οποίας στερεώνεται μια μικρή σημειακή μάζα m=0,2kg, η οποία απέχει απόσταση d=0,4m από το άκρο Α της ράβδου. Στο άκρο Α ή στο Β πρέπει να στηρίξουμε κατακόρυφα τη ράβδο στην παλάμη μας για να πετύχουμε καλύτερη ισορροπία, με την έννοια ότι αν εκτραπεί λίγο από την κατακόρυφο, θα αποκτήσει μικρότερη γωνιακή επιτάχυνση;

Απάντηση:

Πότε έχουμε καλύτερη ισορροπία

Υπολογισμός δύναμης από τον άξονα περιστροφής μιας ράβδου.

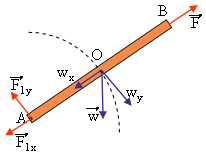
Μια ομογενής δοκός ΑΒ μήκους 0,6m και μάζας m=10kg στρέφεται γύρω από οριζόντιο άξονα που περνά από το άκρο της Α. Τη στιγμή που βρίσκεται στη θέση του σχήματος, όπου ημθ=0,8 η δοκός έχει γωνιακή ταχύτητα ω=10rad/s, με φορά ίδια με την φορά που στρέφονται οι δείκτες του ρολογιού. Για την θέση αυτή να υπολογισθούν:

α) Η γωνιακή επιτάχυνση της δοκού.

β) Οι συνιστώσες F₁ και F₂ της δύναμης που δέχεται η ράβδος από τον άξονα περιστροφής.

Δίνεται η ροπή αδράνειας της δοκού ως προς τον άξονα περιστροφής της Ι= 1/3 ml² και g=10m/s².

Απάντηση:

Δυναμική στερεού με σταθερό άξονα περιστροφής.

Μια ομογενής ράβδος μήκους 1m και μάζας 4kg στρέφεται γύρω από σταθερό οριζόντιο άξονα που περνά από το ένα της άκρο Α. Τη στιγμή που βρίσκεται στη θέση που φαίνεται στο σχήμα, όπου συνθ=0,8, ο άξονας ασκεί δύναμη κάθετη στη ράβδο

Ζητούνται για τη θέση αυτή:

i)  Η γωνιακή ταχύτητα περιστροφής,

ii) Η γωνιακή επιτάχυνση της ράβδου.

iii) Η δύναμη από τον άξονα περιστροφής.

Δίνεται η ροπή αδράνειας της ράβδου ως προς τον άξονα περιστροφής Ι= 1/3 mℓ² και g=10m/s².

Απάντηση:

Δυναμική στερεού με σταθερό άξονα περιστροφής.

Εκτόξευση τροχού σε οριζόντιο επίπεδο, χωρίς γωνιακή ταχύτητα.

Ένας τροχός εκτοξεύεται σε οριζόντιο επίπεδο με το οποίο παρουσιάζει συντελεστή τριβής ολίσθησης μ, με αρχική ταχύτητα υ₀ και χωρίς να στρέφεται. Δίνεται η ροπή αδράνειάς του τροχού ως προς τον άξονα περιστροφής του Ι= ½ m.R². Να χαρακτηρίστε σαν σωστές ή λαθεμένες τις παρακάτω προτάσεις, δικαιολογώντας την απάντησή σας.

α) Ο τροχός δέχεται δύναμη τριβής με φορά προς τα αριστερά και μέτρο Τ=μmg.

β) Η επιβράδυνση του κέντρου Ο του τροχού είναι ίση με μg.

γ) Η γωνιακή επιτάχυνση του τροχού είναι ίση με α_γων= 2μg/R.

δ) Η τριβή μηδενίζεται μόλις η ταχύτητα του κέντρου Ο του τροχού γίνει υ= υ₀/3 .

Απάντηση:

Κύλιση και ολίσθηση τροχού σε λείο επίπεδο.

Γύρω από έναν ομογενή κύλινδρο ο οποίος ηρεμεί σε λείο οριζόντιο επίπεδο, τυλίγουμε ένα αβαρές νήμα. Για t=0 ασκούμε στο άκρο Α του νήματος μια σταθερή οριζόντια δύναμη F.
Δίνεται η ροπή αδράνειάς του κυλίνδρου ως προς τον άξονα περιστροφής του Ι= ½ mR².
Να χαρακτηρίστε σαν σωστές ή λαθεμένες τις παρακάτω προτάσεις, δίνοντας σύντομες επεξηγήσεις:

α) Η επιτάχυνση του άξονα του κυλίνδρου είναι ίση με a_cm=F/m.

β) Η γωνιακή επιτάχυνση του κυλίνδρου συνδέεται με την επιτάχυνση του άξονα με τη σχέση a_cm= α_γων.R.

γ) Η επιτάχυνση του σημείου Α είναι τριπλάσια από την επιτάχυνση του άξονα του κυλίνδρου.

δ) Ο ρυθμός μεταβολής της στροφορμής του κυλίνδρου παραμένει σταθερή.

Απάντηση:

Κύλιση και ολίσθηση τροχού.

Ο εικονιζόμενος κύλινδρος κυλίεται ολισθαίνοντας. Ποια από τις προτάσεις για τη δύναμη τριβής είναι η σωστή :

α. Επιταχύνει και την περιστροφική και την μεταφορική κίνηση

β. Επιβραδύνει και την περιστροφική και την μεταφορική κίνηση

γ. Επιταχύνει την περιστροφική και επιβραδύνει την μεταφορική κίνηση

δ. Επιταχύνει την μεταφορική κίνηση και επιβραδύνει την περιστροφική κίνηση.

Απάντηση:

Τροχαλία και σώματα.

Στο διπλανό σχήμα δίνεται m₂>m₁. Χαρακτηρίστε τις παρακάτω προτάσεις σαν σωστές ή λαθεμένες δίνοντας σύντομες εξηγήσεις.

α) Αν η τροχαλία είναι αβαρής, τότε Τ₁΄=Τ₂΄.

β) Αν το νήμα είναι αβαρές Τ₁=Τ₁΄.

γ) Αν η τροχαλία έχει μάζα Μ και το σχοινί δεν γλιστράει στο αυλάκι της, τότε:

i) Οι μάζες m₁ και m₂ έχουν την ίδια επιτάχυνση.

ii) Το βάρος w₂>Τ₂΄.

iii) Η Τ₂΄είναι μεγαλύτερη από την Τ₁΄.

iv) Η επιτάχυνση της μάζας m₂ συνδέεται με την γωνιακή επιτάχυνση της τροχαλίας με τη σχέση a=α_γωνKR.

Απάντηση:

Διατήρηση Ορμής - Στροφορμής.

Σε ένα λείο οριζόντιο επίπεδο ηρεμεί μια σανίδα μάζας m=10kg. Σε μια στιγμή τοποθετούμε πάνω της ένα τροχό ακτίνας R=0,5m και μάζας m=10kg, ο οπoίος στρέφεται με γωνιακή ταχύτητα ω = -8rad/s, όπως στο σχήμα. Ο συντελεστής τριβής μεταξύ τροχού και σανίδας είναι μ=0,8.

Ποιες προτάσεις είναι σωστές και ποιες λάθος:

α) Ο τροχός θα κινηθεί προς τα δεξιά.

β) Η σανίδα θα κινηθεί προς τα αριστερά.

γ) Η ορμή του συστήματος θα παραμείνει σταθερή.

δ) Η στροφορμή του συστήματος θα παραμείνει σταθερή.

ε) Η μηχανική ενέργεια του συστήματος παραμένει σταθερή.

στ) Ο ρυθμός μεταβολής της στροφορμής του τροχού παραμένει σταθερός.

Απάντηση

Διατήρηση Ορμής-Στροφορμής.

Τι βλέπουν τα μάτια μας;

Ένα όμορφο – αξιοθαύμαστο αρχείο σε Powerpoint. Μια ευγενική προσφορά από τον φίλο και συνάδελφο Άρη. Κατεβάστε το και δείτε το, αξίζει.

ΕΔΩ.

Συνολική ροπή και ανατροπή.

Σε οριζόντιο επίπεδο ηρεμεί ένας κύβος μάζας 100kg και ακμής α=2m. Σε μια στιγμή ασκούμε στο κέντρο του μια οριζόντια δύναμη F=300Ν. Οι συντελεστές τριβής μεταξύ του κύβου και του επιπέδου είναι μ=μ_s=0,2.

i) Ποιες προτάσεις είναι σωστές και ποιες λάθος:

α) Ο κύβος παραμένει ακίνητος.

β) Ο κύβος ισορροπεί.

γ) Η τριβή, είναι τριβή ολίσθησης με μέτρο Τ=200Ν.

δ) Ο κύβος επιταχύνεται προς τα δεξιά με επιτάχυνση α=1m/s².

ε) Ο κύβος ανατρέπεται.

στ) Αφού ο κύβος δεν ανατρέπεται η συνολική ροπή των δυνάμεων ως προς οποιοδήποτε σημείο είναι ίση με μηδέν.

ζ) Ο φορέας της κάθετης αντίδρασης του επιπέδου έχει μοχλοβραχίονα ως προς το κέντρο Ο, ίσο με x=0,2m.

ii) Υπολογίστε την συνολική ροπή ως προς την κορυφή Γ και σχολιάστε το αποτέλεσμα.

Απάντηση:

Υπολογισμός ροπής δύναμης.

Η ράβδος ΑΓ ισορροπεί στηριζόμενη σε κατακόρυφο τοίχο, όπως στο σχήμα.

α) Η ροπή του βάρους ως προς το σημείο Γ είναι τ= mg(ΚΓ).

β) Η ροπή της Ν₁ ως προς το άκρο Γ είναι τ= - Ν₁·(ΑΓ).

γ) Η ροπή της Ν₁ ως προς το άκρο Γ είναι τ= - Ν₁·(ΑΟ).

δ) Το επίπεδο είναι λείο.

Απάντηση:

ΖΕΥΓΟΣ ΔΥΝΑΜΕΩΝ ΚΑΙ ΘΕΜΕΛΙΩΔΗΣ ΝΟΜΟΣ ΤΗΣ ΣΤΡΟΦΙΚΗΣ ΚΙΝΗΣΗΣ.

Η ράβδος ΑΓ του σχήματος έχει μάζα m=3kg, μπορεί να περιστρέφεται γύρω από οριζόντιο άξονα που περνά από το μέσον της Ο. Σε μια στιγμή ασκούνται πάνω της δύο σταθερού μέτρου δυνάμεις F₁=F₂=4Ν κάθετες συνεχώς στη ράβδο, όπως στο σχήμα, όπου (ΑΜ)= (ΜΟ)=1m. Ποιες προτάσεις είναι σωστές και ποιες λάθος:

α) Η ράβδος δέχεται από τον άξονα κατακόρυφη δύναμη με φορά προς τα πάνω και μέτρο F=30Ν.

β) Η ράβδος στρέφεται με σταθερή γωνιακή επιτάχυνση και με φορά ίδια με τους δείκτες του ρολογιού.

γ) Η μέγιστη γωνιακή επιτάχυνση της ράβδου είναι στην οριζόντια θέση και η ελάχιστη στην κατακόρυφη.

δ) Η στροφορμή της ράβδου μετά από χρόνο 5s έχει μέτρο με 20kg·m²/s.

ε) Ο ρυθμός μεταβολής της στροφορμής της ράβδου είναι σταθερή με μέτρο 4kg·m²/s².

στ) Κατά τη στιγμή που η ράβδος έχει στραφεί κατά γωνία θ=10rad έχει κινητική ενέργεια 40J.

ζ) Ο ρυθμός μεταβολής της κινητικής ενέργειας της ράβδου είναι σταθερός.

Δίνεται g=10m/s².

Απάντηση:

ΙΣΟΡΡΟΠΙΑ ΡΑΒΔΟΥ ΚΑΙ ΡΟΠΕΣ

Η ράβδος του σχήματος ισορροπεί οριζόντια δεμένη στο άκρο της με νήμα. Η δύναμη που δέχεται η ράβδος στο άκρο Α από την άρθρωση είναι:

α) Η F1

β) η F2

γ) η F3

δ) η F4

Εξηγείστε γιατί απορρίπτονται οι άλλες περιπτώσεις.

Απάντηση:

ΙΣΟΡΡΟΠΙΑ ΡΑΒΔΟΥ ΚΑΙ ΤΡΙΒΗ

Η ράβδος του σχήματος έχει μήκος 4m και μάζα m=30kg, μπορεί να στρέφεται γύρω από οριζόντιο άξονα που περνά από το άκρο της Α, ενώ στηρίζεται σε κύλινδρο σε σημείο Μ, που απέχει 1m από το άκρο της Β. Ο συντελεστής τριβής μεταξύ σανίδας και κυλίνδρου είναι μ=0,2, ενώ η γωνία κλίσεως της ράβδου έχει ημθ=0,6. Ο κύλινδρος στρέφεται με σταθερή γωνιακή ταχύτητα ω=1rad/s, γύρω από τον άξονά του.

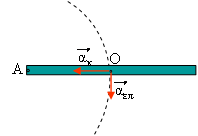
1. Να βρεθούν οι συνιστώσες της δύναμης που ασκείται από τον άξονα στη ράβδο, την F_x παράλληλη προς την ράβδο και F_y κάθετη σ’ αυτήν.
2. Πώς θα μεταβληθεί το μέτρο των παραπάνω συνιστωσών αν αυξήσουμε τη γωνιακή ταχύτητα στην τιμή ω₁=2rad/s;
3. Πώς θα μεταβληθεί το μέτρο των παραπάνω συνιστωσών αντιστραφεί η φορά περιστροφής του κυλίνδρου;

Απάντηση:

.

Ισορροπία στερεού και δύναμη που ασκείται στη σανίδα από ένα κινούμενο σώμα.

Η ράβδος ΑΒ μήκους 4m και βάρους 100Ν μπορεί να στρέφεται γύρω από οριζόντιο άξονα που διέρχεται από το άκρο της Α και ισορροπεί όπως στο σχήμα, δεμένη με νήμα στο άκρο της Β, το οποίο είναι κάθετο σε αυτήν. Κατά μήκος της ράβδου κινείται ένα σώμα Σ μάζας m₁=5kg με επιτάχυνση α=2m/s². Αν η κλίση της σανίδας είναι θ, όπου ημθ=0,6 και συνθ = 0,8, να βρεθούν η τάση του νήματος και οι συνιστώσες της δύναμης που δέχεται η σανίδα από τον άξονα F_x και F_y, όπου η μια έχει την διεύθυνση της σανίδας και η άλλη κάθετη σε αυτήν τη στιγμή που το σώμα περνά από την θέση Ο, απέχοντας 1m από το άκρο B. g=10m/s².

Απάντηση.

Ισορροπία δοκού και η δύναμη από ένα κινούμενο σώμα