ΠΑΝΕΛΛΑΔΙΚΕΣ ΕΞΕΤΑΣΕΙΣ 2008. ΗΛΕΚΤΡΟΛΟΓΙΑ. ΓΕΛ.

them_hlek_kat_c_hmer_no_0806 - Upload a doc

Read this doc on Scribd: them_hlek_kat_c_hmer_no_0806

Μπορείτε να κατεβάσετε τα θέματα από ΕΔΩ.

ΠΑΝΕΛΛΑΔΙΚΕΣ ΕΞΕΤΑΣΕΙΣ ΦΥΣΙΚΗΣ ΚΑΤ. ΓΕΛ.

them_fis_kat_c_hmer_no_0806 - Upload a doc

Read this doc on Scribd: them_fis_kat_c_hmer_no_0806

Μπορείτε όμως και να τα κατεβάσετε από ΕΔΩ.

Αν θέλετε μπορείτε να διαβάσετε και μια κριτική "εν θερμώ" για τα παραπάνω θέματα, επισκεφτείτε

σχολείο και σχόλιο...

.

ΠΑΝΕΛΛΑΔΙΚΕΣ ΕΞΕΤΑΣΕΙΣ.2008. ΦΥΣΙΚΗ ΚΑΤ. ΕΣΠΕΡΙΝΩΝ.

them_fis_kat_d_esp_no_0806 - Upload a doc

Read this doc on Scribd: them_fis_kat_d_esp_no_0806

ΘΕΜΑΤΑ ΦΥΣΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ ΕΣΠΕΡΙΝΩΝ

ΜΠΟΡΕΙΤΕ ΝΑ ΤΑ ΚΑΤΕΒΑΣΕΤΕ ΣΕ pdf ΑΠΟ

ΕΔΩ

ΠΑΝΕΛΛΑΔΙΚΕΣ ΕΞΕΤΑΣΕΙΣ. ΗΛΕΚΤΡΟΛΟΓΙΑ.ΕΣΠΕΡΙΝΑ.

them_hlek_kat_d_esp_no_0806 - Upload a doc

Read this doc on Scribd: them_hlek_kat_d_esp_no_0806

ΘΕΜΑΤΑ ΗΛΕΚΤΡΟΛΟΓΙΑΣ ΕΣΠΕΡΙΝΩΝ
Υπάρχει κανένας ενδιαφερόμενος;;
Μπορείτε να κατεβάσετε τα θέματα από ΕΔΩ.

ΚΑΛΗ ΕΠΙΤΥΧΙΑ

Σε όλους τους μαθητές που στη διάρκεια της χρονιάς διάβασαν, κουράστηκαν, πάλεψαν για τις εξετάσεις, εύχομαι:

ΚΑΛΗ ΕΠΙΤΥΧΙΑ

Να αντιμετωπίσουν με ψυχραιμία τις εξετάσεις αυτές και να τις δουν σαν ένα απλό επεισόδιο στη μάχη της ζωής.

Η ζωή δεν τελειώνει με μια επιτυχία ή αποτυχία σε εξετάσεις...

Τους εύχομαι να είναι καλά στην ΥΓΕΙΑ τους και να μπορέσουν να βρουν το δρόμο τους στη ζωή.

Φιλικά

Διονύσης Μάργαρης.

ΘΕΜΑΤΑ ΠΑΝΕΛΛΑΔΙΚΩΝ ΦΥΣΙΚΗΣ Γ.Π. ΗΜΕΡΗΣΙΩΝ.

Κάποτε όλοι μας, καθηγητές και μαθητές παρακολουθούσαμε και είτε ουσιαστικά είτε ωφελιμιστικά, ασχολούμαστε με το ομορφότερο κομμάτι της Φυσικής του Λυκείου. Τη Φυσική της Γενικής παιδείας. Το μάθημα έγινε ουσιαστικά ενδοσχολικό και τις συνέπειες νομίζω τις γνωρίζουμε όλοι. Μπορεί όμως να απέμεινε και κάποιος;;; που να ενδιαφέρεται.

Ας δει λοιπόν τα θέματα της Γενικής παιδείας των Ημερησίων Λυκείων από ΕΔΩ.

Σαν επανάληψη ακούγεται, του προηγουμένου post...

Με ποια ερώτηση. Υπάρχει κάποια πρόταση για το πώς μπορούμε να κάνουμε τους μαθητές μας της Γ΄Λυκείου να ενδιαφερθούν για το μάθημα της Γενικής παιδείας;;; Και δεν υπονοώ να το κάνουμε υποχρεωτικό στις Πανελλαδικές...

them_fis_gen_c_hmer_no_0806 - Upload a doc

Read this doc on Scribd: them_fis_gen_c_hmer_no_0806

ΠΑΝΕΛΛΑΔΙΚΕΣ. ΦΥΣΙΚΗ ΓΕΝΙΚΗΣ ΕΣΠΕΡΙΝΩΝ.

Κάποτε όλοι μας, καθηγητές και μαθητές παρακολουθούσαμε και είτε ουσιαστικά είτε ωφελιμιστικά, ασχολούμαστε με το ομορφότερο κομμάτι της Φυσικής του Λυκείου. Τη Φυσική της Γενικής παιδείας. Το μάθημα έγινε ουσιαστικά ενδοσχολικό και τις συνέπειες νομίζω τις γνωρίζουμε όλοι. Μπορεί όμως να απέμεινε και κάποιος;;; που να ενδιαφέρεται.

Ας κατεβάσει λοιπόν τα θέματα της Γενικής παιδείας των Εσπερινών Λυκείων από

ΕΔΩ.

ή ας τα δει μόνο...

them_fis_gen_d_esp_no_0806 - Upload a doc

Read this doc on Scribd: them_fis_gen_d_esp_no_0806

Στροφορμή υλικού σημείου.

Μια προσπάθεια για ξεκαθάρισμα σε απορία μαθητή μου…

Ένα υλικό σημείο κινείται πάνω στο επίπεδο xy με ταχύτητα υ, όπως στο σχήμα.

Ποιες προτάσεις είναι σωστές και ποιες λάθος:

1. Η στροφορμή του υλικού σημείου κατά τον άξονα x είναι L=mυr.
2. Η στροφορμή του υλικού σημείου κατά τον άξονα x είναι L=mυ·(AO).
3. Η στροφορμή του υλικού σημείου ως προς τον άξονα y είναι μηδέν.
4. Η στροφορμή του υλικού σημείου κατά τον άξονα z που είναι κάθετος στο επίπεδο στο σημείο Ο, έχει μέτρο L=mυr.
5. Η στροφορμή του υλικού σημείου κατά τον άξονα z που είναι κάθετος στο επίπεδο στο σημείο Ο, έχει μέτρο L=mυ·(ΑΟ).
6. Η στροφορμή του υλικού σημείου κατά τον άξονα z που είναι κάθετος στο επίπεδο στο σημείο Ο, είναι κάθετη στο επίπεδο xy, με φορά προς τα μέσα.

Μια εφαρμογή:

Ο δίσκος του σχήματος στρέφεται γύρω από τον κατακόρυφο άξονά του που περνά από το κέντρο του, με γωνιακή ταχύτητα ω. Ένα υλικό σημείο πέφτει ελεύθερα και σε μια στιγμή έχει ταχύτητα υ, όπως στο σχήμα. Πόση είναι η συνολική στροφορμή του συστήματος κατά τον άξονα περιστροφής του δίσκου;

Απάντηση:

Στροφορμή υλικού σημείου

.

Ταλάντωση σε πλάγιο επίπεδο και κρούση.

Το σώμα Α μάζας m₁=2kg ηρεμεί σε κεκλιμένο επίπεδο κλίσεως θ=30°, δεμένο στο άκρο ελατηρίου σταθεράς Κ=200Ν/m. Το σώμα Α δεν εμφανίζει τριβές με το επίπεδο. Μετακινούμε το σώμα συσπειρώνοντας το ελατήριο κατά d=0,5m και το αφήνουμε να κινηθεί.

1)   Να αποδειχθεί ότι το σώμα Α θα εκτελέσει απλή αρμονική ταλάντωση.

2)   Πόση ενέργεια καταναλώσαμε για την μετακίνηση του σώματος Α κατά d.

3)  Μετά από μετατόπιση του σώματος Α κατά s=0,9m, συγκρούεται μετωπικά και ελαστικά με άλλο σώμα Β μάζας m₂=1kg, το οποίο ήταν ακίνητο. Μετά την κρούση το σώμα Β διανύει απόσταση 0,8m κατά μήκος του επιπέδου.

i)   Να βρεθεί η τριβή που ασκήθηκε στο σώμα Β κατά την κίνησή του.

ii)  Να υπολογισθεί η ενέργεια ταλάντωσης του σώματος Α μετά την κρούση.

iii) Να εξετασθεί αν τα δύο σώματα θα ξανασυγκρουσθούν.

Δίνεται g=10m/s².

Απάντηση:

Μια ταλάντωση σε πλάγιο επίπεδο και κρούση.

Ταλάντωση συστήματος σωμάτων

.

Τις τελευταίες μέρες δύο μαθητές μου με ρώτησαν για απορίες τους πάνω στην άσκηση 1.46 του σχολικού βιβλίου. Με αφορμή τις ερωτήσεις αυτές και επειδή φαντάζομαι ότι παρόμοιες απορίες θα έχουν και άλλοι μαθητές, ας δούμε τι συμβαίνει, με την βοήθεια κάποιων ερωτήσεων πάνω στην εξέλιξη της κίνησης των σωμάτων.

Το σύστημα των σωμάτων Α και Β με μάζες m₁ και m₂ εφάπτονται μεταξύ τους και ηρεμούν σε λείο οριζόντιο επίπεδο, ενώ το σώμα Α είναι δεμένο στο άκρο οριζόντιου ελατηρίου, σταθεράς Κ, όπως στο σχήμα. Σπρώχνουμε το σώμα Β συσπειρώνοντας το ελατήριο κατά Α και αφήνουμε το σύστημα να ταλαντωθεί.

Α) Ποιες προτάσεις είναι σωστές και ποιες λάθος.

1. Το σύστημα εκτελεί α.α.τ. με σταθερά D=Κ.
2. Το σώμα Α εκτελεί α.α.τ. με σταθερά D=Κ.
3. Το σώμα Α εκτελεί α.α.τ. επειδή δέχεται την δύναμη του ελατηρίου με μέτρο F_ελ=Κ·Δl=K·x.
4. Το σώμα Β δέχεται δύναμη από το ελατήριο και γι’ αυτό θα κινηθεί προς τα δεξιά.

Β) Το σώμα Β δέχεται οριζόντια δύναμη F₂₁ από το σώμα Α η οποία δίνεται από την εξίσωση:

i) F21= - Κ·x	ii) F21= - D2·x
iii) F21= - m2ω2·x	iv) F21= - m2·Kx /(m1+m2)
v) F21= m2α

Ποιες από τις παραπάνω σχέσεις είναι σωστές;

Γ) Σε ποια θέση μηδενίζεται η δύναμη F₂₁;

Δ) Τι κίνηση θα εκτελέσει κάθε σώμα μετά την θέση x=0 και γιατί;

Ε) Μόλις αποχωριστούν τα δύο σώματα:

1. Το σώμα Α θα συνεχίσει να εκτελεί α.α.τ. με την ίδια περίοδο.
2. Το σώμα Α θα συνεχίσει να εκτελεί α.α.τ. με σταθερά D=Κ.
3. Η μέγιστη ταχύτητα του σώματος Α δεν θα αλλάξει.
4. Η μέγιστη δύναμη που δέχεται το σώμα Α από το ελατήριο θα μεταβληθεί.
5. Η ενέργεια ταλάντωσης του σώματος Α δεν θα μεταβληθεί.

Απάντηση:

Ταλάντωση και σύστημα σωμάτων. Πού αποχωρίζονται;

Έργο δύναμης- ροπής και Κινητική Ενέργεια.

Το ομοαξονικό σύστημα των δύο κυλίνδρων με ακτίνες R₁=0,1m και R₂=0,5m ηρεμεί σε οριζόντιο επίπεδο. Τυλίγουμε γύρω από τον κύλινδρο ακτίνας R₁ ένα αβαρές νήμα, ασκώντας στο άκρο του Α οριζόντια δύναμη F=40Ν. Το σύστημα αρχίζει να κυλίεται χωρίς να ολισθαίνει. Για μετακίνηση κατά x=10m του άξονα των κυλίνδρων, να βρεθούν:

1. Το έργο της δύναμης F.
2. Η κινητική ενέργεια του συστήματος των δύο κυλίνδρων.

Απάντηση:

Τάση του νήματος και επιτάχυνση.

Η ομογενής ράβδος ΑΒ του σχήματος, έχει μάζα Μ και μήκος L, συνδέεται στο άκρο της Α σε άρθρωση και ισορροπεί οριζόντια δεμένη στο άκρο νήματος στο σημείο Μ, όπου (ΑΜ)= ¾ L , ενώ στο άκρο της Β κρέμεται με άλλο νήμα σώμα Σ μάζας ½ Μ. Δίνεται η ροπή αδράνειας της ράβδου ως προς το άκρο Α, Ι = 1/3 ΜL².

Α) Ποιες προτάσεις είναι σωστές και ποιες λάθος:

1. Στην ράβδο ασκούνται 3 δυνάμεις. Μια από το νήμα η Τ₁, το βάρος της W και το βάρος του Σ.
2. Η δύναμη που ασκείται στο άκρο Β από το νήμα είναι κατακόρυφη και ίση με το βάρος του Σ.
3. Η τάση Τ₁ έχει μέτρο Τ₁= Μg+Μg/2= 3/2 Μg.

Β) Σε μια στιγμή κόβουμε τι νήμα (1). Αν Ι η ροπή αδράνειας της ράβδου ως προς το άκρο Α, τότε αμέσως μετά η ράβδος αποκτά γωνιακή επιτάχυνση που υπολογίζεται από τη σχέση:

1. W·L/2 + W₁·L/2= Ι·α_γων.
2. W·L/2 + Τ·L/2= Ι·α_γων, όπου Τ η τάση του νήματος (2).
3. W·L/2 = Ι·α_γων.

Γ) Η επιτάχυνση του σημείου Β είναι μεγαλύτερη, ίση ή μικρότερη από την επιτάχυνση του σώματος Σ;

Απάντηση:

Τάση του νήματος και επιτάχυνση

.

Συχνότητα-μήκος κύματος και φαινόμενο Doppler.

Το Σάββατο 19/4 απευθυνόμενος στους μαθητές μου και αναφερόμενος σε μια συζήτηση που έγινε την προηγούμενη στην τάξη, έγραψα το άρθρο Οδηγίες προς ναυτιλομένους... για το ποιες Ασκήσεις πρέπει να προσέξουν. Τόνιζα επίσης ότι στο τελευταίο χρονικό διάστημα να μην ασχοληθούν προσπαθώντας να λύσουν δύσκολες Ασκήσεις.

Χθες διάβασα ένα άρθρο που απευθύνεται σε συναδέλφους, από τον συνάδελφο Γιώργο Παναγιωτακόπουλο με παρόμοιο θέμα. Προτείνω στους συναδέλφους να το διαβάσουν.

Στο ίδιο Blog όμως διάβασα και μια πολύ καλή και σύντομη ανάλυση για το Φαινόμενο Doppler… Αυτό θα το συνιστούσα σε καθηγητές και σε μαθητές να το μελετήσουν.

Με αφορμή τα όσα γράφει ο συνάδελφος, ας δούμε ένα παράδειγμα.

Ένα τραίνο κινείται με ταχύτητα υ₁=20m/s σε ευθύγραμμο δρόμο και έχει σειρήνα που παράγει ήχο συχνότητας f_s=3600Ηz. Αν η ταχύτητα του ήχου στον αέρα είναι υ=340m/s, να βρεθούν:

Α) Το μήκος κύματος που εκπέμπεται από την πηγή, όταν είναι ακίνητη.

Β) Η συχνότητα και το μήκος κύματος του ήχου που ακούει:

1. Ο παρατηρητής Α που βρίσκεται ακίνητος στην άκρη των γραμμών.
2. Ο παρατηρητής Β που είναι πάνω στο τραίνο.

Απάντηση:

Για αυτούς που ήρθαν, αλλά και για αυτούς που απουσιάζουν…

.
Πάνω σε ένα ερώτημα που έθεσε ο Νίκος στην τάξη και σε μια Άσκηση που ζήτησε να λύσουμε.

1. Η ομογενής ράβδος του σχήματος έχει μάζα Μ=30kg, μήκος l =5m και μπορεί να στρέφεται γύρω από οριζόντιο άξονα, ο οποίος διέρχεται από το άκρο της Ο. Η ράβδος ισορροπεί οριζόντια, όταν δεθεί στο άκρο της Α, μέσω νήματος, το οποίο αφού το περάσουμε από τροχαλία μάζας m₃=10kg και ακτίνας R=0,4m, κρεμάσουμε στο άλλο άκρο του σώμα Σ₁ μάζας m₁=5kg, το οποίο συνδέεται με δεύτερο νήμα με ένα άλλο σώμα Σ₂ μάζας m₂=2kg, το οποίο είναι δεμένο στο πάνω άκρο ενός κατακόρυφου ελατηρίου σταθεράς Κ=200Ν/m.

Α) Βρείτε την επιμήκυνση του ελατηρίου.
Β) Σε μια στιγμή κόβουμε το νήμα που συνδέει τα σώματα Σ₁-Σ₂. Για αμέσως μετά το κόψιμο του νήματος, να βρεθούν:

1. Η επιτάχυνση του σώματος Σ₁.
2. Η γωνιακή επιτάχυνση της τροχαλίας και της ράβδου.
3. Η ενέργεια ταλάντωσης του σώματος Σ₂.

Δίνονται οι ροπές αδράνειας ως προς τους άξονες περιστροφής τους, της τροχαλίας Ι_cm= 1/2 mR² και της ράβδου Ι_cm= 1/3 Μl ² και g=10m/s².

Απάντηση:

.

Πτώση και ΑΑΤ.

Τα σώματα Σ και Β αφήνονται να πέσουν ελεύθερα δεμένα στα άκρα ενός ελατηρίου που έχει το φυσικό του μήκος l₀=0,8m και σταθερά Κ=100Ν/m. Το Β απέχει αρχικά κατά h= 15cm από το έδαφος. Η κρούση του σώματος Β με το έδαφος είναι πλαστική και το σώμα κολλά στο έδαφος, ενώ το σώμα Σ που έχει μάζα m=1kg, αρχίζει να εκτελεί απλή αρμονική ταλάντωση. Να βρείτε:

i)   Το πλάτος της ταλάντωσης του σώματος Σ.

ii)  Την ελάχιστη απόσταση μεταξύ των δύο σωμάτων.

iii) Τον ρυθμό μεταβολής της ορμής του σώματος Σ τη στιγμή της ελάχιστης απόστασης.

Δίνεται g=10m/s².

Απάντηση:

Πτώση και ΑΑΤ

Φθίνουσα- και Εξαναγκασμένη Ταλάντωση. Ερωτήσεις με δικαιολόγηση.

1. Ένα σώμα εκτελεί φθίνουσα ταλάντωση και σε μια στιγμή περνά από το σημείο Ρ κατευθυνόμενο προς τη θέση ισορροπίας Ο. Να σχεδιάστε την δύναμη επαναφοράς και τη δύναμη απόσβεσης στη θέση Ρ.
2. Το φορτίο του πυκνωτή σε κύκλωμα RLC μεταβάλλεται όπως στο παραπάνω διάγραμμα. Να σχεδιάστε το διάγραμμα της έντασης του ρεύματος που διαρρέει το κύκλωμα σε συνάρτηση με το χρόνο.
   
3. Ένα σύστημα με ιδιοσυχνότητα f₀=15Ηz τίθεται σε εξαναγκασμένη ταλάντωση με την επίδραση εξωτερικής δύναμης συχνότητας f₁=20Ηz. Αν η συχνότητα της εξωτερικής δύναμης γίνει ίση με f₂=25Ηz, πώς θα μεταβληθούν:
   α. η ιδιοσυχνότητα του συστήματος.
   β. το πλάτος της ταλάντωσης,
   γ. η συχνότητα της ταλάντωσης.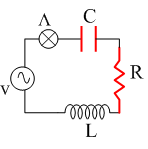
4. Το κύκλωμα του σχήματος κάνει εξαναγκασμένη ταλάντωση σε συντονισμό. Στην αντίσταση R συνδέουμε παράλληλα μια όμοια αντίσταση^. τότε η φωτοβολία του λαμπτήρα :

   α) μειώνεται β) αυξάνεται γ) δεν μεταβάλλεται

Απαντήσεις:
.

Φθίνουσα- Εξαναγκασμένη Ταλάντωση

Α)Ποια πρόταση είναι σωστή σε μια φθίνουσα ταλάντωση:

1. Το πλάτος ταλάντωσης παραμένει σταθερό.
2. Η περίοδος μειώνεται εκθετικά με το χρόνο.
3. Όταν αυξάνεται η σταθερά απόσβεσης, αυξάνεται το πλάτος ταλάντωσης.
4. Όταν μειώνεται η σταθερά απόσβεσης, το πλάτος μειώνεται πιο αργά.

Β)Στο κύκλωμα απεικονίζεται ηλεκτρική ταλάντωση. Για τη χρονική στιγμή αυτή:

1. ο πυκνωτής εκφορτίζεται
2. η ενέργεια του κυκλώματος αυξάνεται
3. η ενέργεια του πηνίου μειώνεται.
4. η ενέργεια του κυκλώματος μειώνεται.

Γ) Σε μια φθίνουσα ταλάντωση, ποιες προτάσεις είναι σωστές:

1. η περίοδος της ταλάντωσης για συγκεκριμένη σταθερά απόσβεσης είναι σταθερή
2. για πολύ μεγάλες αποσβέσεις η κίνηση είναι απεριοδική
3. η ολική ενέργεια της ταλάντωσης παραμένει σταθερή
4. όταν αυξάνεται ο συντελεστής απόσβεσης τότε η συχνότητα μειώνεται
5. το πλάτος παραμένει σταθερό

Δ) Κατά τον συντονισμό ( Ποιες προτάσεις είναι σωστές και ποιες λάθος)

1. το πλάτος είναι μέγιστο
2. η ενέργεια του συστήματος είναι μέγιστη
3. οι απώλειες ενέργειας είναι μέγιστες
4. η ιδιοσυχνότητα του συστήματος είναι μέγιστη
5. η περίοδος είναι μέγιστη

Ε) Η ιδιοσυχνότητα ενός ταλαντωτή εξαρτάται

1. από το πλάτος της ταλάντωσης..
2. από τη σταθερά απόσβεσης.
3. από την αρχική φάση.
4. από τα φυσικά χαρακτηριστικά του συστήματος.

Απαντήσεις:

Κρούση και τριβές.

Το σώμα Α μάζας m₁=2kg, εκτοξεύεται με αρχική ταχύτητα υ₀=6m/s από απόσταση x₁=5m προς ακίνητο σώμα Β μάζας m₂=2kg. Το σώμα Β ηρεμεί στο άκρο ελατηρίου σταθεράς k=200Ν/m και φυσικού μήκους l₀=1m, το άλλο άκρο του οποίου είναι δεμένο σε σώμα Γ. Η ταχύτητα του σώματος Α έχει την διεύθυνση του άξονα του ελατηρίου. Το σώμα Β δεν εμφανίζει τριβές με το επίπεδο, ενώ για τα δύο άλλα σώματα έχουμε μ=μ_s=0,2.

1. Με ποια ταχύτητα το σώμα Α φτάνει στο σώμα Β;
2. Αν η κρούση των δύο σωμάτων είναι μετωπική και ελαστική, να βρεθεί η ελάχιστη μάζα που πρέπει να έχει το σώμα Γ, ώστε να μην μετακινηθεί.
3. Ποιες θα είναι τελικά οι αποστάσεις μεταξύ των σωμάτων, όταν ακινητοποιηθούν;

Απάντηση:

Κρούση και τριβές

Στάσιμο κύμα και στιγμιότυπα.

Στο πάνω σχήμα δίνεται ένα στιγμιότυπο ενός στάσιμου κύματος τη στιγμή t₁, ενώ στο κάτω σχήμα φαίνεται το στιγμιότυπο του ίδιου τη στιγμή t₁+ Τ/4.

1. Ποιες οι ταχύτητες των σημείων Β και Γ τη στιγμή t₁;
2. Σχεδιάστε τις ταχύτητες των σημείων Β και Γ στο κάτω διάγραμμα.
3. Ποια η διαφορά φάσης μεταξύ των σημείων Β και Γ;
4. Σχεδιάστε ένα στιγμιότυπο του ίδιου στάσιμου κύματος τη χρονική στιγμή t₁+ Τ/2.

Απάντηση

Στάσιμο κύμα και στιγμιότυπα

Εξίσωση κύματος και στιγμιότυπο.

Στην άκρη Ο ενός γραμμικού ομογενούς μέσου υπάρχει πηγή κύματος η οποία αρχίζει να ταλαντώνεται για t=0 έχοντας y=0 και αρνητική ταχύτητα. Δίνεται το πλάτος του παραγόμενου κύματος Α=0,2m, ενώ η περίοδος ταλάντωσης Τ=2s και η ταχύτητα του κύματος υ=1m/s.

1. Ποια η εξίσωση της απομάκρυνσης y=f(t) της πηγής;
2. Βρείτε την εξίσωση του κύματος που παράγεται.
3. Σχεδιάστε στιγμιότυπα του κύματος τις χρονικές στιγμές t1=1,5s και t2=2,5s.

Απάντηση:

Εξισώσεις κυμάτων και άλλες.

.

Ποια από τις παρακάτω εξισώσεις αντιστοιχεί σε τρέχων κύμα, ποια σε στάσιμο κύμα και ποια σε απλή αρμονική ταλάντωση. Αυτή που περισσεύει, σε τι αντιστοιχεί;

1.  y = 4 συν(πx) ημ(0,1πt)
   
2.  y = 3 συν(π) ημ2π(4t-0,2x)
   
3.  y = 5 συν(πt) ημ(101πt)
   
4.  y = 0,1 συν(π) ημ(8πt)
   

 .
Απάντηση:

.

Κύλινδρος σε επαφή με δοκό.

Ο κύλινδρος του σχήματος έχει ακτίνα R= 0,4m και μπορεί να στρέφεται γύρω από σταθερό οριζόντιο άξονα, ο οποίος ταυτίζεται με τον άξονά του που περνά από τα κέντρα των δύο βάσεών του. Τυλίγουμε γύρω του ένα αβαρές νήμα, στο άκρο του οποίου δένουμε ένα σώμα Σ μάζας m=1kg και το αφήνουμε να κινηθεί από ύψος h=8m, από το έδαφος.

1. Αν ο χρόνος πτώσης του σώματος Σ είναι t₁=4s, να βρεθεί η ροπή αδράνειας του κυλίνδρου.
2. Πάνω στον κύλινδρο τοποθετούμε μια ομογενή δοκό μήκους l και μάζας m₁=6kg, η οποία συνδέεται σε άρθρωση στο άκρο της Α και στον κύλινδρο στο σημείο Μ, όπου (ΑΜ)= 3l/4. Επαναλαμβάνουμε το πείραμα αφήνοντας για t=0 το σώμα Σ να πέσει από το ίδιο ύψος h. Για t=2s και ενώ το σώμα Σ έχει κατέβει κατά y₁=1m, τοποθετούμε στο άκρο Β ένα σώμα Σ₁ μάζας m₂, το οποίο θεωρείται υλικό σημείο, οπότε το σώμα Σ φτάνει στο έδαφος για t=7s. Ζητούνται:

α) Ο συντελεστής τριβής μεταξύ δοκού και κυλίνδρου.

β) Το βάρος του σώματος Σ₁.

Δίνεται g=10m/s².

Απάντηση:

Ταλάντωση και δύο ελατήρια.

Τα σώματα Α και Β με μάζες m₁=1kg και m₂=3kg ηρεμούν σε λείο οριζόντιο επίπεδο δεμένα στα άκρα δύο οριζόντιων ελατηρίων με σταθερές Κ₁=100Ν/m και Κ₂=50Ν/m αντίστοιχα, απέχοντας απόσταση d=0,3m,όπως στο σχήμα. Εκτρέπουμε το σώμα Α προς τα αριστερά κατά Α=0,5m και το αφήνουμε να ταλαντωθεί. Μετά από λίγο συγκρούεται πλαστικά με το σώμα Β. Ζητούνται:

1. Η ταχύτητα του σώματος Α πριν την κρούση και η κοινή ταχύτητα των σωμάτων αμέσως μετά την κρούση.
2. Η ενέργεια ταλάντωσης μετά την κρούση.

Απάντηση:

Φαινόμενο Doppler και εξετάσεις.

Περιπολικό αυτοκίνητο του οποίου η σειρήνα παράγει ήχο συχνότητας 2900Ηz, καταδιώκει μοτοσικλετιστή. Η κίνηση και των δυο είναι ευθύγραμμη ομαλή. Όταν το περιπολικό και ο μοτοσικλετιστής απέχουν 200m, ο μοτοσικλετιστής διαπιστώνει ότι ο ήχος της σειρήνας έχει συχνότητα 3100Ηz/ Αν μετά από 10s το περιπολικό φτάνει τον μοτοσικλετιστή, να βρεθούν:

1. Οι ταχύτητες των δύο κινητών.
2. Η συχνότητα του ήχου που θα ακούει ο μοτοσικλετιστής, αν μετά το προσπέρασμα σταματήσει, ενώ το περιπολικό εξακολουθεί να κινείται με την ίδια ταχύτητα.

Δίνεται υ_ηχ=340m/s

Εξετάσεις 1980

Απάντηση:

Διάθλαση και ολική ανάκλαση.

Έχω την αίσθηση ότι οι μαθητές μας δυσκολεύονται αρκετά σε ασκήσεις Γεωμετρικής οπτικής. Ίσως να φταίει η υποβάθμιση της Γεωμετρίας στα πλαίσια των Μαθηματικών. Δεν ξέρω, μπορεί να είναι και άλλοι οι λόγοι...
Σε μια προσπάθεια να ξεκολλήσουν, ας δουν δύο ασκήσεις με διάθλαση και ανάκλαση..

Η γωνία Α του πρίσματος είναι ίση με 30°. Μια ακτίνα προσπίπτει στο σημείο Δ υπό γωνία θ, με ημθ=2/3. Αν ο δείκτης διάθλασης του πρίσματος για την παραπάνω ακτίνα είναι ίσος με 4/3, να χαράξετε την πορεία της ακτίνας, μέχρι την έξοδό της από το πρίσμα.

Απάντηση.

Διάθλαση-Ολική ανάκλαση

Διάθλαση ακτίνας

Ένα ορθογώνιο τριγωνικό πρίσμα έχει κάθετες πλευρές (ΑΒ)= 8cm και (ΑΓ) = 6 cm. Μια μονοχρωματική ακτίνα με μήκος κύματος λ₀=400nm προσπίπτει στο σημείο Δ, όπου (ΑΔ)=3 cm, υπό γωνία θ=Γ στην πλευρά ΑΒ. Ο δείκτης διάθλασης του πρίσματος για την ακτινοβολία αυτή είναι n= 4/3, ζητούνται:

1. Να χαραχθεί η πορεία της ακτίνας, μέχρι την έξοδό της από το πρίσμα.
2. Με πόσα μήκη κύματος της ακτινοβολίας στο πρίσμα, αντιστοιχεί η διαδρομή της ακτίνας στο εσωτερικό του;

Απάντηση.

Διάθλαση ακτίνας

Ροπή από τον άξονα και ενέργειες.

Αναφερόμενοι στην Άσκηση: Ροπή από τον άξονα.

Ας δούμε και κάποιες ακόμη ερωτήσεις:

Α) Ποιες προτάσεις είναι σωστές και ποιες λαθεμένες:

1. Το έργο του βάρους του σώματος Σ ισούται με την αύξηση της κινητικής του ενέργειας.
2. Το έργο του βάρους ισούται με την μείωση της δυναμικής ενέργειας του σώματος Σ.
3. Το έργο της τάσης του νήματος εκφράζει την ενέργεια που αφαιρείται από το σώμα Σ και μεταφέρεται μέσω του νήματος στην τροχαλία.
4. Η κινητική ενέργεια που αποκτά η τροχαλία είναι ίση με το έργο της ροπής της Τ΄.
5. Ο ρυθμός μεταβολής της κινητικής ενέργειας της τροχαλίας, είναι ίσος με την ισχύ της Τ΄συν την ισχύ της ροπής της τριβής.

Β) Για την χρονική στιγμή t₁=3s να βρεθούν:

1. Ο ρυθμός μεταβολής της δυναμικής ενέργειας του σώματος Σ.
2. Η ισχύς του βάρους και της τάσης Τ.
3. Ο ρυθμός μεταβολής της κινητικής ενέργειας του σώματος Σ.
4. Η ισχύς της Τ΄και ο ρυθμός μεταβολής της κινητικής ενέργειας της τροχαλίας.

Να σχολιαστούν τα αποτελέσματα.

Απάντηση:

Ροπή από τον άξονα.

Γύρω από μια τροχαλία μάζας 4kg και ακτίνας R=0,1m τυλίγουμε ένα αβαρές νήμα στο άκρο του οποίου δένουμε ένα σώμα Σ μάζας m₁=0,4kg, το οποίο αφήνουμε να κινηθεί από ύψος h=8m από το έδαφος. Ο χρόνος πτώσης είναι t₁=4s. Δίνεται ότι μεταξύ τροχαλίας και του άξονα περιστροφής της αναπτύσσεται σταθερή δύναμη τριβής. Ζητούνται:

1. Η επιτάχυνση του σώματος Σ και η γωνιακή επιτάχυνση της τροχαλίας.
2. Η ροπή που ασκείται στην τροχαλία εξαιτίας της τριβής που αναπτύσσεται μεταξύ τροχαλίας και άξονα της τροχαλίας.
3. Με ποιο ρυθμό η μηχανική ενέργεια μετατρέπεται σε θερμότητα την χρονική στιγμή t=3s;

Δίνεται για την τροχαλία Ι= ½ ΜR² και g=10m/s².

Απάντηση:

Σύνθετη κίνηση και Doppler.

Ο τροχός ενός αυτοκινήτου ακτίνας R=0,5m, το οποίο κινείται ευθύγραμμα με σταθερή ταχύτητα υ=10m/s κυλίεται χωρίς να ολισθαίνει. Το αυτοκίνητο πλησιάζει έναν ακίνητο παρατηρητή ο οποίος βρίσκεται σε μεγάλη απόσταση. Σε σημείο Α του τροχού που απέχει r=0,4m από το κέντρο Ο του τροχού, έχει στερεωθεί μια ηχητική πηγή που εκπέμπει ήχο συχνότητας f=1000/17Ηz και για t=0 βρίσκεται στη θέση που φαίνεται στο σχήμα.

1. Να βρείτε την εξίσωση της ταχύτητας με την οποία η ηχητική πηγή πλησιάζει τον παρατηρητή και να κάνετε την γραφική της παράσταση.
2. Ποια η περίοδος του ήχου που ακούει ο παρατηρητής σε συνάρτηση με το χρόνο; Να γίνει η γραφική παράσταση Τ=f(t).

Δίνεται η ταχύτητα του ήχου στον αέρα υ=340m/s.

Απάντηση:

Μια σύνθετη κίνηση ηχητικής πηγής.