To Θ.Μ.Κ.Ε., η Α.Δ.Μ.Ε και η Α.Δ.Ε. Πότε ισχύουν;

Πλησιάζοντας προς τις εξετάσεις, οι μαθητές μας πρέπει να ξεκαθαρίσουν τα βασικά. Υπάρχει σε πολλούς ένα μπλέξιμο σχετικά με διατήρηση ενέργειας, ΘΜΚΕ κλπ. Υπήρξε και μια προτροπή από ένα μαθητή, για κάτι ανάλογο. Ελπίζοντας λοιπόν να βοηθήσει έστω και ένα υποψήφιο, δίνω μια σύντομη παρουσίαση του θέματος.

1) Το θεώρημα μεταβολής της κινητικής ενέργειας (Θ.Μ.Κ.Ε) ή αλλιώς το θεώρημα έργου-ενέργειας:

 

α) Εφαρμόζεται για ένα σώμα.

β) Ισχύει ΠΑΝΤΑ, ανεξάρτητα από το είδος των ασκουμένων δυνάμεων.

γ) Το ΘΜΚΕ μπορεί να εφαρμοστεί σε κάθε περίπτωση αλλά ορισμένες φορές δεν μας βοηθά στη λύση ενός προβλήματος, όπως π.χ. στις εξής δύο περιπτώσεις:

i) Αν στα δεδομένα ή στα ζητούμενα εμπλέκεται ο χρόνος (αυτό δεν σημαίνει. ότι σε συνδυασμό με άλλες εξισώσεις, δεν μπορεί να χρησιμοποιηθεί και το ΘΜΚΕ, αλλά από μόνο του δεν δίνει λύση).

ii) Αν μελετάμε ένα σύστημα σωμάτων που αλληλεπιδρούν. Αυτό, στην περίπτωση που δεν μπορούμε να υπολογίσουμε το έργο της δύναμης αλληλεπίδρασης για το ένα σώμα.

 

Παράδειγμα 1°:

Ένα σώμα Σ μάζας 4kg ηρεμεί σε λείο κεκλιμένο επίπεδο, κλίσεως θ=30°, δεμένο στο κάτω άκρο ενός ιδανικού ελατηρίου σταθεράς k=200Ν/m. Σε μια στιγμή ένα δεύτερο σώμα που κινείται προς τα πάνω, συγκρούεται ελαστικά με το σώμα Σ. Αν το σώμα Σ μετακινηθεί κατά 0,2m πριν σταματήσει στιγμιαία, ποια η ταχύτητα του σώματος Σ αμέσως μετά την κρούση;

Δίνεται g=10m/s².

Απάντηση:

 

Παράδειγμα 2°:

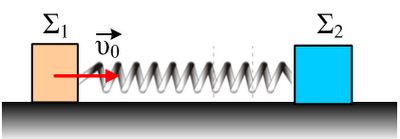
Δύο σώματα Σ₁, Σ₂ με μάζες m₁=2kg και m₂=3kg ηρεμούν σε λείο οριζόντιο επίπεδο, δεμένα στα άκρα ιδανικού ελατηρίου σταθεράς k=480 Ν/m. Κάποια στιγμή κτυπάμε το Σ₁, το οποίο αποκτά αρχική ταχύτητα υ₀=10m/s με κατεύθυνση προς το Σ₂. Να βρεθεί η ταχύτητα του Σ₁, όταν το ελατήριο έχει συσπειρωθεί κατά Δl=0,5m.

Απάντηση:

 

2) Η αρχή διατήρησης της μηχανικής ενέργειας (Α.Δ.Μ.Ε.)

 

α) Εφαρμόζεται για ένα σύστημα σωμάτων και όχι για ένα σώμα.

β) Ισχύει ΜΟΝΟ, αν οι όλες οι δυνάμεις που παράγουν έργο, είναι συντηρητικές(Διατηρητικές).

i) Αν ένα σώμα κινείται στο βαρυτικό πεδίο της Γης, μέλος του συστήματος είναι και η Γη, αλλά συνήθως το «ξεχνάμε», μιας και η μεταβολή της δυναμικής ενέργειας του συστήματος σώμα-Γη, συνδέεται με την κινητική ενέργεια του σώματος. Έτσι λέμε «η δυναμική ενέργεια του σώματος» πράγμα που ενώ δεν είναι σωστό, ίσως απλοποιεί τα πράγματα και διευκολύνει τους μαθητές.

ii) Όταν εφαρμόζουμε την ΑΔΜΕ, μπορεί να ασκούνται διάφορες δυνάμεις στο σύστημά μας, που να μην είναι συντηρητικές. Αρκεί οι δυνάμεις αυτές να μην παράγουν έργο.

 

 

Παράδειγμα 3°:

Να λυθεί το 1° παράδειγμα με εφαρμογή της ΑΔΜΕ.

 

Απάντηση:

 

Παράδειγμα 4°:

Να απαντηθεί το 2° παράδειγμα με χρήση της ΑΔΜΕ.

 

Απάντηση:

 

3) Η αρχή διατήρησης της ενέργειας (Α.Δ.Ε.)

 

α) Εφαρμόζεται για ένα σύστημα σωμάτων που μπορεί να είναι και το ΣΥΜΠΑΝ όλο.

β) Ισχύει ΠΑΝΤΑ.

 

Σχόλιο:

Στην πραγματικότητα τα πράγματα έχουν ακριβώς την αντίθετη σειρά. Η ΑΔΕ είναι μια γενική αρχή διατήρησης, που ισχύει σε όλες τις Φυσικές επιστήμες, χωρίς καμιά εξαίρεση, αν και σύμφωνα με την σύγχρονη Φυσική επεκτείνεται ώστε να συμπεριλάβει και την ύλη, έτσι ώστε σήμερα να μιλάμε για διατήρηση της υλοενέργειας.

Η διατήρηση της μηχανικής ενέργειας, είναι μια υποπερίπτωση της ΑΔΕ, όταν έχουμε μόνο συντηρητικές δυνάμεις, ενώ το Θ,Μ.Κ.Ε. είναι αυτό που λέει το όνομά του.

Ένα θεώρημα, που εφαρμόζεται για ένα σώμα και συνδέει τα έργα των δυνάμεων που ασκούνται πάνω του με την μεταβολή της κινητικής του ενέργειας.

 

Παράδειγμα 5°:

Πάνω σε ένα μη λείο οριζόντιο επίπεδο ηρεμεί ένας τροχός μάζας Μ=20kg και ακτίνας R=0,6m. Σε μια στιγμή δέχεται στο κέντρο του μια σταθερή οριζόντια δύναμη F μέτρου 100Ν, όπως στο σχήμα. Όταν ο τροχός έχει περιστραφεί κατά γωνία θ=15rad, το κέντρο Ο του τροχού, έχει μετατοπισθεί κατά x=18m.

i) Πόση ενέργεια μετεφέρθη στον τροχό, μέσω της δύναμης F;

ii) Πόση θερμότητα παρήχθη εξαιτίας της τριβής;

Για τον τροχό δίνεται Ι= ½ ΜR².

Απάντηση:

 

 

Υ.Γ.

Δηλαδή ποτέ δεν εφαρμόζουμε το Θ.Μ.Κ.Ε. αν έχουμε ένα σύστημα σωμάτων;

Δεν είπα αυτό. Λέω απλά ότι, συνήθως έχουμε πρόβλημα να υπολογίσουμε το έργο της δύναμης αλληλεπίδρασης. Αν μπορούμε να το υπολογίσουμε, δεν υπάρχει πρόβλημα, πολύ δε περισσότερο αν μας ζητάνε το έργο. Τότε ναι, εφαρμόζουμε το Θ.Μ.Κ.Ε. Να τονίσω στο σημείο αυτό ότι τα έργα των εσωτερικών δυνάμεων δεν είναι πάντα αντίθετα. Οι δυνάμεις είναι αντίθετες, όχι τα έργα τους.

 

Παράδειγμα 6°:

Σε λείο οριζόντιο επίπεδο ηρεμεί σώμα Σ μάζας Μ=9kg. Σε μια στιγμή ένα βλήμα μάζας m=1kg που κινείται οριζόντια με ταχύτητα υ₀=100m/s, σφηνώνεται στο σώμα Σ.

α) Να υπολογιστούν τα έργα:

i) Της δύναμης που ασκήθηκε στο σώμα Σ από το βλήμα.

ii) Της αντίδρασής της, που ασκήθηκε στο βλήμα.

β) Να υπολογισθεί η απώλεια μηχανικής ενέργειας στη διάρκεια της κρούσης. Πώς συνδέεται αυτή με τα έργα των παραπάνω δυνάμεων;

 

Απάντηση:

Διαβάστε όλο το αρχείο, μαζί με τις ενδιάμεσες απαντήσεις, με κλικ εδώ ή και εδώ.

Για μια αναλυτικότερη μελέτη, δείτε μια προσφορά του συναδέλφου Σταύρου Πρωτογεράκη από ΕΔΩ. Σε ευχαριστώ Σταύρο για την προσφορά.

.