Κύμα κατά μήκος δύο νημάτων.

Κατά μήκος ενός σχοινιού (α) διαδίδεται ο κυματοσυρμός του πρώτου σχήματος και μετά από λίγο φτάνει στο σχοινί (β), όπου η ταχύτητα του κύματος είναι μικρότερη.

i) Ποιο από τα παρακάτω σχήματα είναι σωστό; Να δικαιολογήστε την απάντησή σας.

ii) Γιατί το πλάτος κατά την επιστροφή είναι μικρότερο;

Απάντηση:

Κύμα κατά μήκος δύο νημάτων

Δύο εικόνες που δείχνουν το τι ακριβώς συμβαίνει στην παραπάνω περίπτωση:

Ηλεκτρομαγνητικό Κύμα. ΗΜΚ.

Δίνονται τα πιο κάτω ζεύγη εξισώσεων όπου Ε η ένταση ηλεκτρικού πεδίου και Β η ένταση μαγνητικού πεδίου:

α. Ε = 75 ημ 2π (12⋅10¹⁰t – 4⋅10⁴x)
Β = 25⋅10^-8ημ 2π (12⋅10¹⁰t – 4⋅10⁴x) (SI)

β. Ε = 300 ημ 2π (6⋅10¹⁰t – 2⋅10²x)
Β = 100⋅10^-8 ημ 2π (6⋅10¹⁰t – 2⋅10²x) (SI)

γ. Ε = 150 ημ 2π (9⋅10¹⁰t – 3⋅10²x)
Β = 50⋅10^-8 ημ 2π (9⋅10¹⁰t + 3⋅10² x) (SI)

Ποιο από τα παραπάνω ζεύγη περιγράφει ηλεκτρομαγνητικό κύμα που διαδίδεται στο κενό;

Να αιτιολογήσετε την απάντησή σας.

Εξετάσεις Ε.Λ. 2005

Απαντήσεις

Στάσιμο κύμα και διαφορά φάσης.

Κατά μήκος ενός γραμμικού ελαστικού μέσου διαδίδεται ένα εγκάρσιο αρμονικό κύμα με εξίσωση y₁= 0,1 ημ(πt-πx). (1)

i)  Ποια η διαφορά φάσης μεταξύ δύο σημείων Β και Γ τα οποία βρίσκονται στις θέσεις x₁=0,75m και x₂=1m.

ii) Να σχεδιάσετε στιγμιότυπα του κύματος τις χρονικές στιγμές t₁= 3,5s και t₂= 4s.

Το παραπάνω κύμα συμβάλλει με ένα δεύτερο κύμα που κινείται αντίθετα με εξίσωση:

y₂= 0,1 ημ(πt+πx) (2)

iii) Ποια η εξίσωση του στάσιμου κύματος που δημιουργείται;

iv) Βρείτε τη διαφορά φάσεως μεταξύ των σημείων Β και Γ και σχεδιάστε στιγμιότυπα του στάσιμου τις χρονικές στιγμές t₁= 3,5s και t₂= 4s, δεχόμενοι ότι για t=0 έχει δημιουργηθεί το στάσιμο σε μια περιοχή μήκους 3,5m.

.

Απαντήσεις

Στάσιμο κύμα  και διαφορά φάσης

Συμβολή κυμάτων πάνω στην ευθεία που ενώνει τις δύο πηγές.

.

Σε δύο σημεία μιας ευθείας ε βρίσκονται δύο σύγχρονες πηγές κυμάτων Ο₁ και Ο₂ οι οποίες παράγουν κύματα με πλάτος Α=2cm και μήκος κύματος λ=8m. Η απόσταση των δύο πηγών είναι d=20m.

1.     Να βρεθεί το πλάτος ταλάντωσης ενός σημείου Σ της ευθείας ε, που βρίσκεται εκτός του ευθύγραμμου τμήματος Ο₁Ο₂.

2.     Ποιο το πλάτος ταλάντωσης σημείου Ρ που βρίσκεται μεταξύ των δύο πηγών και απέχει 6m από την πηγή Ο₂;

3.      Πόσα σημεία της ευθείας ε ταλαντώνονται με μέγιστο πλάτος;

.

Απάντηση:

.

Κύματα και προς τις δύο κατευθύνσεις.

.

Στη θέση x=0 ενός γραμμικού ομογενούς ελαστικού μέσου υπάρχει πηγή κύματος η οποία αρχίζει να ταλαντώνεται σύμφωνα με την εξίσωση y= 0,2ημπt (μονάδες στο S.Ι.) Το κύμα που δημιουργείται διαδίδεται και προς τις δύο κατευθύνσεις με ταχύτητα υ=1m/s.

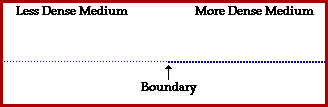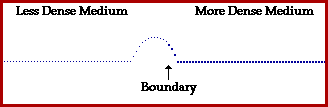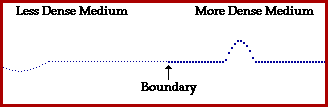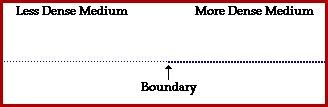
i) Να βρείτε τις εξισώσεις των δύο κυμάτων που δημιουργούνται.

ii) Να σχεδιάστε τη μορφή του ελαστικού μέσου τις χρονικές στιγμές t₁=1s και t₂=1,5s.

Απάντηση:

Αρχική φάση κύματος.

.

Ένα αρμονικό κύμα διαδίδεται προς τη θετική κατεύθυνση με ταχύτητα υ=2m/s και για t=0 το σημείο Ο στη θέση x=0 βρίσκεται για πρώτη φορά στην μέγιστη θετική απομάκρυνσή του. Δίνεται το πλάτος ταλάντωσης του σημείου Ο, Α=0,3m και η περίοδός του Τ=2s.

1. Βρείτε την εξίσωση του κύματος
   
2. Να κάνετε τη γραφική παράσταση της φάσης των διαφόρων σημείων του μέσου σε συνάρτηση με την απόστασή τους από την πηγή τη χρονική στιγμή t₁=2,5s.
   
3. Να δώσετε το στιγμιότυπο του κύματος τη χρονική στιγμή t₁.
   

.
Απάντηση.

Αρχική φάση κύματος

.

ΚΥΜΑΤΑ. Φάση και διαφορά φάσης.

.Κατά μήκος ενός γραμμικού ελαστικού μέσου και από αριστερά προς τα δεξιά διαδίδεται ένα κύμα και στο παρακάτω σχήμα δίνεται το  στιγμιότυπο του κύματος για t₀=0, ενώ τη χρονική στιγμή t₁=0,5s το αντίστοιχο στιγμιότυπο είναι αυτό του διπλανού σχήματος.

1.     Να βρεθεί η εξίσωση του κύματος.

2.     Να κάνετε τη γραφική παράσταση της φάσης των διαφόρων σημείων του μέσου δεξιά της θέσης x=0 για t=1,5s, 
3.     Να κάνετε τη γραφική παράσταση της φάσης ενός σημείου Γ που βρίσκεται στη θέση x=0,8m σε συνάρτηση με το χρόνο.

4.     Βρείτε μια εξίσωση που παρέχει τη διαφορά φάσης μεταξύ δύο σημείων Γ και Δ του μέσου.

5.      Ποια η απόσταση μεταξύ των σημείων Γ και Δ, αν μεταξύ τους παρουσιάζουν διαφορά φάσης 2π;

. .
Απάντηση:

Σύνθεση Ταλαντώσεων και κρούση.

Σώμα Σ₁ μάζας m₁=1kg εκτελεί ταυτόχρονα δύο απλές αρμονικές ταλαντώσεις που έχουν την ίδια οριζόντια διεύθυνση και γίνονται γύρω από την ίδια θέση ισορροπίας. Οι εξισώσεις των δύο ταλαντώσεων σε συνάρτηση με το χρόνο είναι:

α) Να γράψετε την εξίσωση της συνισταμένης ταλάντωσης που εκτελεί το σώμα Σ₁.

β) Τη χρονική στιγμή t₁= π/5 s το σώμα Σ₁ συγκρούεται μετωπικά και πλαστικά με σώμα Σ₂ μάζας m₂=0,5kg που κινείται προς την αντίθετη κατεύθυνση από το σώμα Σ₁ με ταχύτητα μέτρου υ₂=1m/s. Το συσσωμάτωμα που προκύπτει εκτελεί α.α.τ. της ίδιας διεύθυνσης γύρω από την ίδια θέση ισορροπίας.

i) Να προσδιορίσετε την ταχύτητα του σώματος Σ₁ ελάχιστα πριν την κρούση.

ii) Να βρείτε την κοινή ταχύτητα του συσσωματώματος αμέσως μετά την κρούση.

iii) Η ενέργεια ταλάντωσης μετά την κρούση είναι:

Α) Ε= ½ m₁·υ_κ² + ½ m₁·ω² ·x₁² = 6,5J

Β) Ε= ½ (m₁ +m₂)·υ_κ² + ½ m₁·ω² ·x₁² = 6,75 J

Γ) Ε= ½ (m₁ +m₂)·υ_κ² + ½ (m₁+m₂)·ω² ·x₁² =9,75 J

Επιλέξτε την σωστή απάντηση.

Απάντηση:

ΚΡΟΥΣΗ ΚΑΙ ΤΑΛΑΝΤΩΣΗ.

Μια σφαίρα μάζας m=1kg εκτοξεύεται για t=0 με ταχύτητα υ₁ από το σημείο Β, το οποίο απέχει απόσταση s=3m από ακίνητο σώμα Σ, το οποίο ηρεμεί δεμένο στο άκρο οριζόντιου ελατηρίου σταθεράς k=20Ν/m. Μετά από λίγο η σφαίρα συγκρούεται μετωπικά με το σώμα Σ, το οποίο μετά την κρούση εκτελεί α.α.τ. με εξίσωση x=(2/π) ημ(πt-π) (μονάδες S.Ι.). Αν το επίπεδο είναι λείο και η διάρκεια της κρούσεως αμελητέα, η προς τα δεξιά κατεύθυνση θετική, ενώ π²≈10, ζητούνται:

i) Η ταχύτητα υ₁ της σφαίρας.

ii) Ποια χρονική στιγμή η σφαίρα θα ξαναπεράσει από το σημείο Β.

iii) Πόσο θα απέχουν μεταξύ τους τη στιγμή αυτή τα δύο σώματα;

Απάντηση:

ΚΡΟΥΣΗ ΚΑΙ ΤΑΛΑΝΤΩΣΗ

Μηχανικό σύστημα - Ελαστική κρούση.

Στο σχή­μα το σώ­μα Γ κι­νεί­ται ο­ρι­ζό­ντια με τα­χύ­τη­τα υ₀=3m/s και για t=0 συ­γκρού­ε­ται με­τω­πι­κά και ε­λα­στι­κά με το σώ­μα Β. Αν m_Α=m_Β=2m_Γ= 2kg και το ε­λα­τή­ριο έ­χει φυ­σι­κό μή­κος 0,5m και στα­θε­ρά Κ=128N/m, ζη­τού­νται: 

1)  Η τα­χύ­τη­τα του σώ­μα­τος Β με­τά την κρού­ση. 

2)  Η ε­λά­χι­στη α­πό­στα­ση με­τα­ξύ των σω­μά­των Α και Β. 

3)  Ποι­α χρο­νι­κή στιγ­μή το Α θα α­πο­σπα­σθεί α­πό τον τοί­χο. 

4)  Ποι­α η δύ­να­μη που δέ­χε­ται το σώ­μα Α α­πό τον τοί­χο, σε συ­νάρ­τη­ση με τον χρό­νο, αν η κρούση έγινε για t=0 και είχε αμελητέα διάρκεια. 

5) Η μέ­γι­στη τα­χύ­τη­τα του Α.

Αρ­χι­κά τα σώ­μα­τα Α και Β ή­ταν α­κί­νη­τα και δε­μέ­να με το ε­λα­τή­ριο και το ε­πί­πε­δο εί­ναι λεί­ο.

Απάντηση:

Μηχανικό σύστημα και Ελαστική κρούση

Ελαστική κρούση και δυνάμεις.

Μια σφαίρα Α μάζας m₁=2kg κινείται σε λείο οριζόντιο επίπεδο με ταχύτητα υ₁=10m/s και συγκρούεται κεντρικά ελαστικά με ακίνητη σφαίρα Β μάζας m₂=3kg. Σε μια στιγμή t₁ στη διάρκεια της κρούσης η σφαίρα Β έχει ταχύτητα υ_Β=6m/s.

i) Για τη στιγμή t₁:

α) Πόση κινητική ενέργεια έχει κάθε σφαίρα;

β) Πόση είναι η δυναμική ενέργεια παραμόρφωσης των δύο σφαιρών;

ii) Να βρείτε τα έργα των δυνάμεων που ασκούνται μεταξύ των δύο σωμάτων από την στιγμή t₁ μέχρι το τέλος της κρούσης.

iii) Με βάση τα παραπάνω αποτελέσματα χαρακτηρίστε τις παρακάτω προτάσεις ως σωστές ή λαθεμένες.

α) Κατά τη διάρκεια μιας ελαστικής κεντρικής κρούσης η ορμή του συστήματος παραμένει σταθερή.

β) Κατά τη διάρκεια μιας ελαστικής κεντρικής κρούσης η κινητική ενέργεια του συστήματος παραμένει σταθερή.

γ) Κατά τη διάρκεια μιας ελαστικής κεντρικής κρούσης η ορμή κάθε σφαίρας παραμένει σταθερή.

δ) Η παραμόρφωση των σφαιρών είναι ελαστική.

ε) Τα έργα της δράσης – αντίδρασης είναι αντίθετα.

στ) Οι δυνάμεις που ασκούνται μεταξύ των δύο σφαιρών κατά τη διάρκεια μιας ελαστικής κεντρικής κρούσης είναι συντηρητικές.

Απάντηση:

Ελαστική κρούση, δυνάμεις και τα έργα τους!!!

Διακρότημα και φαινόμενο Doppler.

Αυτοκίνητο κινείται σε ευθύγραμμο δρόμο με ταχύτητα υ₁=40m/s και πλησιάζει κάθετα ένα κατακόρυφο τοίχο. Ένας δρομέας κινείται στην ίδια κατεύθυνση με ταχύτητα υ₂=10m/s. Η σειρήνα του αυτοκινήτου εκπέμπει ήχο συχνότητας f_s=3000Ηz. Αν η ταχύτητα του ήχου ως προς τον ακίνητο αέρα είναι ίση με υ=340m/s, να βρεθούν:

α) Ποια η συχνότητα του ήχου που ανακλάται στον τοίχο.

β) Ποια η συχνότητα του διακροτήματος που ακούει ο δρομέας;

Απάντηση:

Φαινόμενο Doppler και συχνότητες διαφόρων παρατηρητών.

Ένα τρένο κατευθύνεται προς ένα τούνελ και εκπέμπει ήχο συχνότητας f_s. Ο ήχος ανακλάται από τον κατακόρυφο τοίχο.

i) Αν ο ακίνητος παρατηρητής Π₁ ακούει τον ήχο από το τρένο με συχνότητα f₁ και τον ήχο από ανάκλαση με συχνότητα f₁΄, να αποδείξτε ότι f₁=f₁΄.

ii) Αν ο ακίνητος παρατηρητής Π₂ ακούει τον ήχο από το τρένο με συχνότητα f₂ και τον ήχο από ανάκλαση με τον τοίχο με συχνότητα f₂΄, να αποδείξτε ότι:

f₂΄> f_s > f₂.

iii) Αν ο μηχανοδηγός ακούει τον ήχο από ανάκλαση με συχνότητα f_α να αποδείξτε ότι

Απάντηση:

Φαινόμενο Doppler και συχνότητες διαφόρων παρατηρητών

Φαινόμενο Doppler και κίνηση σε διαφορετική διεύθυνση.

Ένας ακίνητος παρατηρητής Α απέχει απόσταση d=60m από ευθύγραμμο δρόμο, στον οποίο κινείται ένα όχημα με σταθερή ταχύτητα υ_s=20m/s. Τη στιγμή που το όχημα περνά από το κοντινότερο προς τον παρατηρητή σημείο αρχίζει να εκπέμπει ήχο συχνότητας f_s=7040Ηz για χρονικό διάστημα t=4s.

i) Ποια η αρχική συχνότητα που ακούει ο παρατηρητής;

ii) Ποια η ελάχιστη συχνότητα του ήχου που αντιλαμβάνεται ο παρατηρητής;
Δίνεται η ταχύτητα του ήχου στον αέρα υ=340m/s.

Απάντηση:

.

Φαινόμενο Doppler

Ένας παρατηρητής κινείται σε ευθύγραμμο δρόμο με σταθερή ταχύτητα υ_Α=20m/s και σε μια στιγμή t=0 και ενώ απέχει d=50m από προπορευόμενη πηγή ήχου, η οποία κινείται με ταχύτητα υ_s=10m/s, ακούει ήχο συχνότητας f₁=3600Ηz.

i) Ποια η συχνότητα του ήχου που παράγει η πηγή;

ii) Ποια συχνότητα θα ακούει ο παρατηρητής τη χρονική στιγμή t₁=10s;
Δίνεται η ταχύτητα του ήχου στον αέρα υ=340m/s.

Απάντηση:

ΦΑΙΝΟΜΕΝΟ DOPPLER

.

Θα ανέβει ο Καλόγερος;

Ένα θέμα από τον διαγωνισμό ΦΥΣΙΚΗΣ 2008

Απάντηση:

Μπείτε να δείτε και όλες τις απαντήσεις:

pan_diag_a_lyk_2008_lys.pdf

pan_diag_b_lyk_2008lys.pdf

pan_diag_c_lyk_2008lys.pdf

Φθίνουσα Ταλάντωση.

Το παραπάνω διάγραμμα δίνει την απομάκρυνση σε συνάρτηση με το χρόνο σε μια φθίνουσα ταλάντωση.
Ποιο από τα επόμενα διαγράμματα δίνει της δύναμη απόσβεσης σε συνάρτηση με το χρόνο;

.
Απάντηση:
.

Διακρότημα.

Ένα ηλεκτρόνιο πραγματοποιεί στην οθόνη ενός παλμογράφου δύο απλές αρμονικές ταλαντώσεις ίδιας διεύθυνσης, γύρω από την ίδια θέση ισορροπίας με εξισώσεις:

y₁= 0,1ημ80πt και y₂= 0,1ημω₂t (S.Ι)

με ω₂ κοντά στην τιμή των 80πrad/s. Ο χρόνος ανάμεσα σε δύο διαδοχικές διαβάσεις του ηλεκτρονίου από τη θέση ισορροπίας του είναι Δt= 1/82 s.

i) Βρείτε την γωνιακή συχνότητα της δεύτερης ταλάντωσης.

ii) Να γράψετε της εξίσωση της συνισταμένης κίνησης και να υπολογίσετε την περίοδο μεταβολής του πλάτους της.

iii) Να υπολογίστε τον αριθμό των ταλαντώσεων που πραγματοποιεί το ηλεκτρόνιο μέσα σε χρονικό διάστημα ίσο με δύο περιόδους μεταβολής του πλάτους του.

Απάντηση:

Σύνθεση Ταλαντώσεων

Ένα υλικό σημείο εκτελεί ταυτόχρονα δύο ταλαντώσεις της ίδιας διεύθυνσης, γύρω από την ίδια θέση ισορροπίας με εξισώσεις: 

y₁= 4ημ(4πt+ 2π/3) και y₂=4ημ(4πt+ π/6) μονάδες στο S.Ι. 

i) Ποιες οι συχνότητες των δύο ταλαντώσεων; 

ii) Ποια η διαφορά φάσης μεταξύ τους; 

iii) Βρείτε την εξίσωση y=f(t) για την απομάκρυνση του υλικού σημείου, σε συνάρτηση με το χρόνο.

Απάντηση:

Σύνθεση Ταλαντώσεων.

Εξαναγκασμένη Ηλεκτρική Ταλάντωση.

Η τάση της γεννήτριας δίνεται από την εξίσωση v=40ημ(4000t + φ ). Δίνεται για το κύκλωμα C=20μF, L=2mΗ και R=0,5Ω ενώ διαρρέεται από ρεύμα πλάτους Ι=0,1A, όπου για t=0, i= - 0,1Α

i)    Ποια η γωνιακή (κυκλική) ιδιοσυχνότητα του Β κυκλώματος;

ii)   Να βρεθεί η εξίσωση της έντασης του ρεύματος που διαρρέει το Β κύκλωμα καθώς και του φορτίου του πυκνωτή, σε συνάρτηση με το χρόνο.

iii)  Να υπολογιστεί η μέγιστη ενέργεια που αποθηκεύεται στο πηνίο και στον πυκνωτή του Β κυκλώματος.

iv)   Πόση θερμότητα παράγεται στον αντιστάτη σε χρονικό διάστημα 20s;

Απάντηση:

ΔΙΑΓΩΝΙΣΜΑ ΦΥΣΙΚΗΣ ΚΑΤ. Γ

Ένας κύλινδρος μάζας m=50kg και ακτίνας R=0,4m ηρεμεί σε τραχύ οριζόντιο δρόμο. Για t=0 σπρώχνεται από ένα παιδί με μια σταθερή οριζόντια δύναμη F=60Ν σε ένα σημείο που απέχει κατακόρυφη απόσταση h=0,5m από το έδαφος, μέχρι τη στιγμή t=10s, όπου φτάνει σε λείο κεκλιμένο επίπεδο, στο οποίο συνεχίζει την κίνησή του, χωρίς να σπρώχνεται από το παιδί. Αν στον οριζόντιο δρόμο ο κύλινδρος κυλίεται χωρίς να ολισθαίνει, γύρω από τον άξονά του για τον οποίο Ι= 1/2 mR² και g=10m/s², ζητούνται:

1. Η επιτάχυνση του άξονα του κυλίνδρου.
2. Ο ρυθμός μεταβολής της στροφορμής του κυλίνδρου για t₁=5s.
3. Η κινητική ενέργεια του κυλίνδρου τη στιγμή που φτάνει στην κορυφή του κεκλιμένου επιπέδου.
4. H ταχύτητα του άξονα του κυλίνδρου, όταν κατέλθει κατακόρυφα κατά h₁=2,2m κατά την κίνησή του στο κεκλιμένο επίπεδο.

Ένας κύλινδρος που σπρώχνεται…

Μπορείτε να δείτε όλο το διαγώνισμα από ΕΔΩ.
.

Διαγράμματα στην α.α.τ.

Ένα σώμα εκτελεί α.α.τ ξεκινώντας από τη θέση x=+Α για t=0.

i) Ποιο από τα παρακάτω διαγράμματα παριστά, την Κινητική, Δυναμική και την Ενέργεια ταλάντωσης σε συνάρτηση με το χρόνο;

ii) Ποιο από τα παρακάτω διαγράμματα παριστά την απομάκρυνση, τη ταχύτητα και την συνισταμένη δύναμη σε συνάρτηση με το χρόνο;

Απάντηση:
.

Απλή Αρμονική Ταλάντωση και διαγράμματα.

Στα άκρα δύο όμοιων οριζόντιων ελατηρίων ηρεμούν τα σώματα Σ₁ και Σ₂ με ίσες μάζες.

Εκτρέπουμε τα σώματα προς τα δεξιά, το Σ₁ κατά Α και το Σ₂ κατά 2Α και για t=0 τα αφήνουμε να κινηθούν εκτελώντας α.α.τ.

i) Στη θέση ισορροπίας θα φτάσει πρώτο το σώμα:

α) Σ1

β) Σ2

γ) θα φτάσουν ταυτόχρονα.

ii) Μεγαλύτερη ταχύτητα θα αποκτήσει το σώμα

α) Σ1

β) Σ2

γ) θα αποκτήσουν ίσες μέγιστες ταχύτητες.

iii) Μεγαλύτερη κατά μέτρο δύναμη επαναφοράς στη διάρκεια της κίνησης, θα δεχτεί
α) το σώμα Σ₁ β) το σώμα Σ₂ γ) θα δεχτούν ίσες δυνάμεις.

iv) Ποιο από τα παρακάτω διαγράμματα παριστά τη δύναμη που δέχεται το σώμα Σ₁ σε συνάρτηση με το χρόνο;

Απάντηση:

Πλαστική κρούση και αλλαγή της θέσης Ισορροπίας Ταλάντωσης.

Ένα σώ­μα Σ μά­ζας Μ=9kg ηρεμεί στο πάνω άκρο κατακόρυφου ε­λα­τη­ρί­ου στα­θε­ράς Κ=100N/m. Α­πό ύ­ψος 5m πά­νω α­πό το σώ­μα Σ, ρί­χνου­με κα­τα­κό­ρυ­φα με αρ­χι­κή τα­χύ­τη­τα υ₀=10m/s έ­να σώ­μα Σ₁ μά­ζας 1kg που σφη­νώ­νε­ται στο σώ­μα Σ. Να βρεί­τε:

1. την κοινή ταχύτητα του συσσωματώματος αμέσως μετά την κρούση
   
2. το πλά­τος της τα­λά­ντω­σης που θα ε­κτε­λέ­σει το σύ­στη­μα των δύ­ο σω­μά­των. g=10m/s².
   

.

 Απάντηση:

.

Ενέργεια Ταλάντωσης

Έ­να σώ­μα μά­ζας m=2kg η­ρε­μεί σε ση­μεί­ο Ο, στο ά­κρο κα­τα­κό­ρυ­φου ε­λα­τη­ρί­ου, στα­θε­ράς k=100Ν/m, το άλ­λο ά­κρο του ο­ποί­ου κρέ­με­ται α­πό στα­θε­ρό ση­μεί­ο. Προσφέροντάς του ενέργεια W=4,5J το απομακρύνουμε κατά Α, φέρνοντάς το στη θέση Γ, οπότε αφήνοντάς το εκτελεί απλή αρμονική ταλάντωση πλάτους Α.

i) Πό­ση εί­ναι η ε­νέρ­γει­α τα­λά­ντω­σης;

ii) Βρείτε το πλάτος ταλάντωσης Α.

iii) Στη θέ­ση Γ τι ε­νέρ­γει­α τα­λά­ντω­σης έ­χου­με;

iv) Πό­ση εί­ναι η δυ­να­μι­κή ε­νέρ­γει­α του ε­λα­τη­ρί­ου στη θέση Γ;

v) Πό­ση εί­ναι η ε­νέρ­γει­α της τα­λά­ντω­σης στην θέ­ση Ο και με ποι­α μορ­φή εμ­φα­νί­ζε­ται;

vi) Έ­χει δυ­να­μι­κή ε­νέρ­γει­α το ε­λα­τή­ριο στην θέ­ση Ο, και αν ναι πό­ση εί­ναι αυ­τή; g=10m/s².

Απάντηση:

Απλή Αρμονική Ταλάντωση.

Έ­να ι­δα­νι­κό ε­λα­τή­ριο στα­θε­ράς 400N/m ι­σορ­ρο­πεί σε κα­τα­κό­ρυ­φη θέ­ση, με το πά­νω ά­κρο του συν­δε­δε­μέ­νο σε α­κλό­νη­το ση­μεί­ο και το κά­τω ά­κρο ε­λεύ­θε­ρο. Στο ε­λεύ­θε­ρο ά­κρο κρε­μά­με σώ­μα Σ μά­ζας 4kg και το α­φή­νου­με να κι­νη­θεί α­πό τη θέ­ση φυ­σι­κού μή­κους του ε­λα­τη­ρί­ου.
Α­πο­δείξ­τε ό­τι το Σ θα ε­κτε­λέ­σει α.α.τ. και βρεί­τε το πλά­τος της ταλάντωσης.
Τρι­βές δεν υ­πάρ­χουν. g=10m/s².

Απάντηση

Πλάγια κρούση.

Μια σφαίρα Α κινείται με ταχύτητα υ σε λείο οριζόντιο επίπεδο και συγκρούεται με ακίνητη σφαίρα Β, ίσης μάζας όπως στο σχήμα. Στο σχήμα βλέπετε τις συνιστώσες της ταχύτητας, υ_x στη διεύθυνση της διακέντρου των δύο σφαιρών και υ_y σε κάθετη διεύθυνση. 

Χαρακτηρίστε σαν σωστές ή λαθεμένες τις παρακάτω προτάσεις.

α)  Μετά την κρούση η Α σφαίρα στον άξονα x θα έχει ταχύτητα με φορά προς τα αριστερά και μέτρο ίσο με υ_x.

β)  Μετά την κρούση η Α σφαίρα στον άξονα y θα έχει ταχύτητα με φορά προς τα πάνω και μέτρο ίσο με υ_y.

γ)  Η σφαίρα Β θα κινηθεί μετά την κρούση στη διεύθυνση x.

δ)  Οι δύο σφαίρες θα κινηθούν σε κάθετες διευθύνσεις.

ε)  Το ποσοστό απώλειας της κινητικής ενέργειας της Α σφαίρας που οφείλεται στην κρούση είναι ίσο με 100συν²θ, όπου θ η γωνία που σχηματίζει η αρχική ταχύτητα με τη διάκεντρο των δύο σφαιρών.

Απάντηση:

Πλάγια ελαστική κρούση

Τάση του νήματος. Πλαστική κρούση.

Σώ­μα Σ μά­ζας 950g κρέ­με­ται α­πό νή­μα μή­κους 2,5m. Βλή­μα μά­ζας 50g που κι­νεί­ται ο­ρι­ζό­ντια με τα­χύ­τη­τα 100m/s σφη­νώ­νε­ται στο Σ.

α) Ποι­α η ε­λά­χι­στη τι­μή του ο­ρί­ου θραύ­σης του νή­μα­τος, ώ­στε αυ­τό να μην σπά­σει;

β) Ποι­α η ε­λά­χι­στη τι­μή της τά­σης του νή­μα­τος;

γ) Ποι­ο το πο­σο­στό της ε­νέρ­γει­ας που έ­γι­νε θερ­μό­τη­τα κα­τά την κρού­ση; g=10m/s².

Απάντηση:

Κοινή ταχύτητα και πλαστική κρούση.

Σε λείο οριζόντιο επίπεδο ηρεμεί σανίδα μάζας Μ= 3kg και μήκους 4m. Από το ένα άκρο της εκτοξεύ­ουμε πάνω της σώμα Σ μάζας m=1kg με ταχύτητα υ₀=4m/s. Αν το μισό τμήμα της σανίδας Α, δεν πα­ρουσιάζει τριβή με τη σφαίρα, ενώ το άλλο μισό Β παρουσιάζει συντελεστή τριβής ολίσθησης μ=0,4 ζητούνται:

i)    Ποια η ταχύτητα της σανίδας, όταν σταματήσει πάνω της το σώμα Σ;

ii)   Πόση απόσταση θα διανύσει το σώμα Σ στο τμήμα Β μέχρι να σταματήσει και βρείτε επίσης την απόσταση που δια νύει η σανίδα μέχρι να σταματήσει να κινείται πάνω της το σώμα Σ,

iii)  Υπολογίστε τα έργα των δυνάμεων που ασκούνται στα σώματα. Υι  ενεργειακές μετατροπές μετράνε τα έργα αυτά;

iv) Ένα σώμα μάζας m=1kg κινείται σε λείο οριζόντιο επίπεδο και συγκρούεται πλαστικά με ακίνητο σώμα μάζας Μ=3kg. Ποια η κοινή ταχύτητα του συσσωματώματος και ποια η απώλεια της Μηχανικής ενέργειας που οφείλεται στην κρούση;

  Δίνεται: g=10m/s²..

Απάντηση:

Κοινή ταχύτητα και πλαστική κρούση

Εξισώσεις απλής αρμονικής ταλάντωσης.

Έ­να υ­λι­κό ση­μεί­ο κά­νει α.α.τ. με πλά­τος 0,1m και στην αρ­χή των χρό­νων, βρί­σκε­ται σε ση­μεί­ο Μ με α­πο­μά­κρυν­ση 5cm, α­πο­μα­κρυ­νό­με­νο α­πό τη θέ­ση ι­σορ­ρο­πί­ας. Με­τά α­πό 1s περ­νά ξα­νά α­πό το Μ για πρώ­τη φο­ρά με α­ντί­θε­τη τα­χύ­τη­τα.

i) Βρεί­τε τις ε­ξι­σώ­σεις της α­πο­μά­κρυν­σης και της τα­χύ­τη­τας σε συ­νάρ­τη­ση με το χρό­νο.

ii) Ποια η εξίσωση της φάσης σε συνάρτηση με το χρόνο; Να κάνετε την γραφική της παράσταση.

Απάντηση:

ΔΙΑΓΩΝΙΣΜΟΣ ΦΥΣΙΚΗΣ 2008

Το σώμα που φαίνεται στο διπλανό σχήμα, αφήνεται πάνω από το οριζόντιο δάπεδο με το οποίο δεν παρουσιάζει τριβή. Στο σχήμα φαίνεται και το κέντρο μάζας Κ του σώματος το οποίο τη στιγμή που αφήνεται το σώμα βρίσκεται σε ύψος h. Αν η κρούση του σώματος με το δάπεδο είναι ελαστική και η αντίσταση του αέρα είναι αμελητέα, ποια από τις παρακάτω προτάσεις είναι σωστή;

α. Το κέντρο μάζας του σώματος μετά την κρούση θα εκτελέσει πλάγια βολή προς τα δεξιά και θα φτάσει σε μικρότερο ύψος από το ύψος h από το οποίο αφέθηκε.

β. Το κέντρο μάζας του σώματος μετά την κρούση θα κινηθεί κατακόρυφα αλλά θα φτάσει σε μικρότερο ύψος από το ύψος h από το οποίο αφέθηκε.

γ. Το κέντρο μάζας του σώματος μετά την κρούση θα εκτελέσει πλάγια βολή προς τα αριστερά και θα φτάσει σε μικρότερο ύψος από το ύψος h από το οποίο αφέθηκε.

δ. Το κέντρο μάζας του σώματος μετά την κρούση θα κινηθεί κατακόρυφα και θα φτάσει σε ίδιο ύψος h από το οποίο αφέθηκε.

ε. Το κέντρο μάζας του σώματος μετά την κρούση θα εκτελέσει πλάγια βολή προς τα δεξιά και θα φτάσει στο ίδιο ύψος h από το οποίο αφέθηκε.

στ. Το κέντρο μάζας του σώματος μετά την κρούση θα εκτελέσει πλάγια βολή προς τα αριστερά και θα φτάσει στο ίδιο ύψος h από το οποίο αφέθηκε.

Να δικαιολογήσετε πλήρως την απάντησή σας.

Απάντηση:

Μπορείτε να δείτε τα θέματα και των τριών τάξεων:

Α΄Τάξη

Β΄Τάξη

Γ΄Τάξη

Μπείτε να δείτε και όλες τις απαντήσεις:

pan_diag_a_lyk_2008_lys.pdf

pan_diag_b_lyk_2008lys.pdf

pan_diag_c_lyk_2008lys.pdf

Μπορείτε να δείτε και μια προσομοίωση με το interactive Physics για το θέμα αυτό, από τον συνάδελφο Σαράντο Οικονομίδη